Reconfigurable FPGA-Based Solvers For Sparse Satellite Control

This paper introduces a novel reconfigurable and power-efficient FPGA (Field-Programmable Gate Array) implementation of an operator splitting algorithm for Non-Terrestial Network's (NTN) relay satellites model predictive orientation control (MPC). Our approach ensures system stability and introduces an innovative reconfigurable bit-width FPGA-based optimization solver. To demonstrate its efficacy, we employ a real FPGA-In-the-Loop hardware setup to control simulated satellite dynamics. Furthermore, we conduct an in-depth comparative analysis, examining various fixed-point configurations to evaluate the combined system's closed-loop performance and power efficiency, providing a holistic understanding of the proposed implementation's advantages.

Improved Convergence Bounds For Operator Splitting Algorithms With Rare Extreme Errors

In this paper, we improve upon our previous work[24,22] and establish convergence bounds on the objective function values of approximate proximal-gradient descent (AxPGD), approximate accelerated proximal-gradient descent (AxAPGD) and approximate proximal ADMM (AxWLM-ADMM) schemes. We consider approximation errors that manifest rare extreme events and we propagate their effects through iterations. We establish probabilistic asymptotic and non-asymptotic convergence bounds as functions of the range (upper/lower bounds) and variance of approximation errors. We use the derived bound to assess AxPGD in a sparse model predictive control of a spacecraft system and compare its accuracy with previously derived bounds.

A Low-Power Hardware-Friendly Optimisation Algorithm With Absolute Numerical Stability and Convergence Guarantees

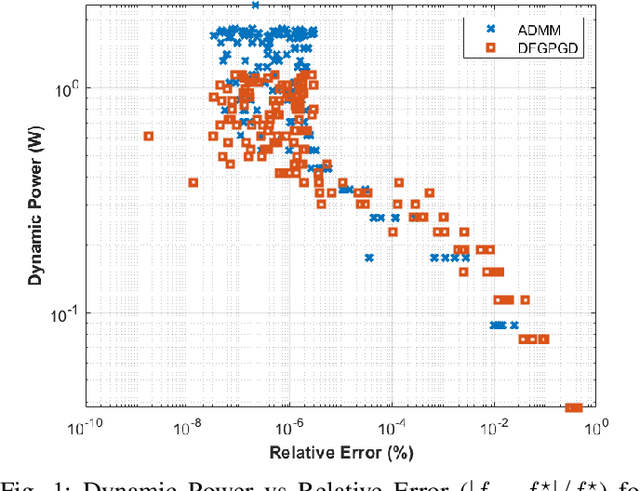
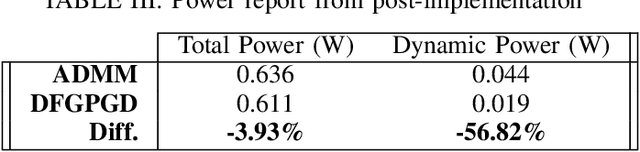
We propose Dual-Feedback Generalized Proximal Gradient Descent (DFGPGD) as a new, hardware-friendly, operator splitting algorithm. We then establish convergence guarantees under approximate computational errors and we derive theoretical criteria for the numerical stability of DFGPGD based on absolute stability of dynamical systems. We also propose a new generalized proximal ADMM that can be used to instantiate most of existing proximal-based composite optimization solvers. We implement DFGPGD and ADMM on FPGA ZCU106 board and compare them in light of FPGA's timing as well as resource utilization and power efficiency. We also perform a full-stack, application-to-hardware, comparison between approximate versions of DFGPGD and ADMM based on dynamic power/error rate trade-off, which is a new hardware-application combined metric.

Probabilistic Verification of Approximate Algorithms with Unstructured Errors: Application to Fully Inexact Generalized ADMM

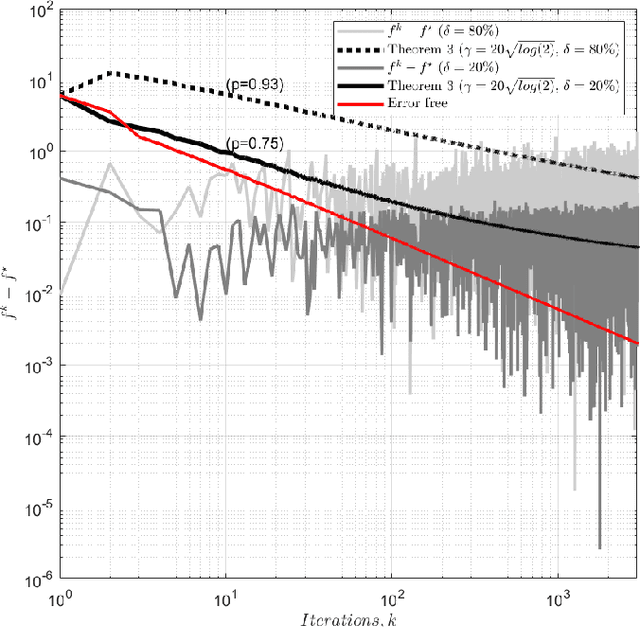
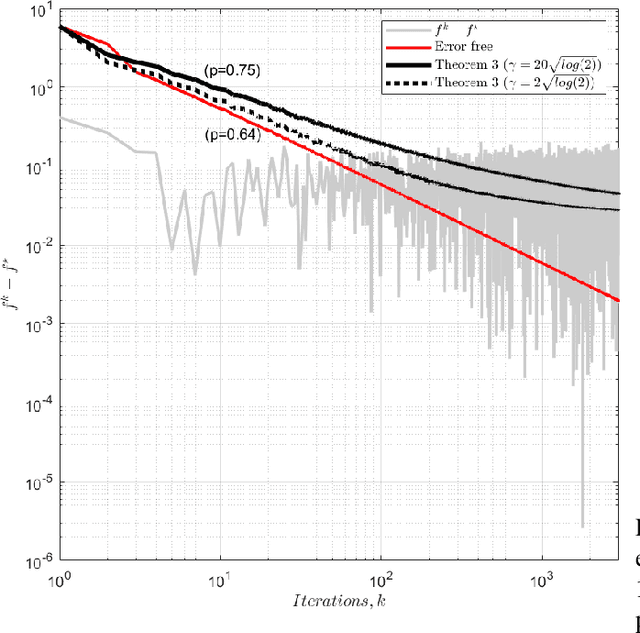
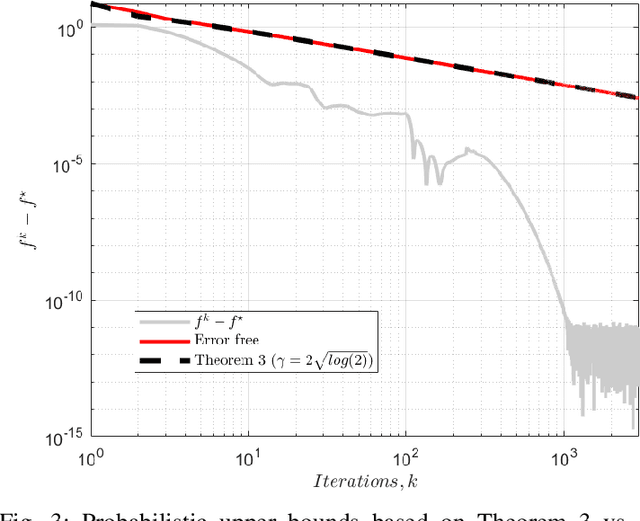
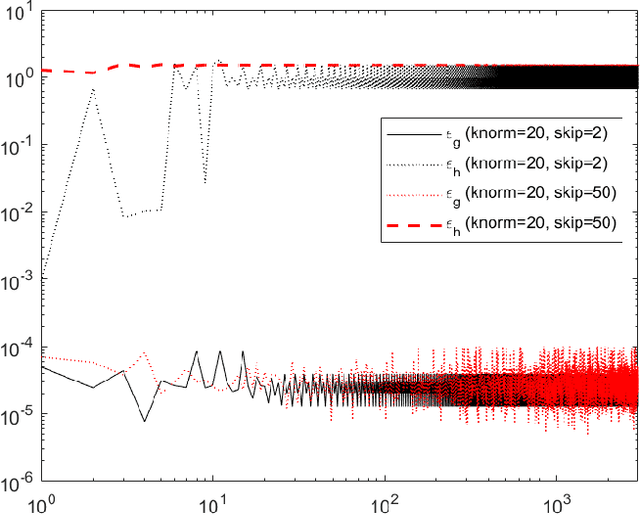
We analyse the convergence of an approximate, fully inexact, ADMM algorithm under additive, deterministic and probabilistic error models. We consider the generalized ADMM scheme that is derived from generalized Lagrangian penalty with additive (smoothing) adaptive-metric quadratic proximal perturbations. We derive explicit deterministic and probabilistic convergence upper bounds for the lower-C2 nonconvex case as well as the convex case under the Lipschitz continuity condition. We also present more practical conditions on the proximal errors under which convergence of the approximate ADMM to a suboptimal solution is guaranteed with high probability. We consider statistically and dynamically-unstructured conditional mean independent bounded error sequences. We validate our results using both simulated and practical software and algorithmic computational perturbations. We apply the proposed algorithm to a synthetic LASSO and robust regression with k-support norm regularization problems and test our proposed bounds under different computational noise levels. Compared to classical convergence results, the adaptive probabilistic bounds are more accurate in predicting the distance from the optimal set and parasitic residual error under different sources of inaccuracies.

Sharper Bounds for Proximal Gradient Algorithms with Errors

We analyse the convergence of the proximal gradient algorithm for convex composite problems in the presence of gradient and proximal computational inaccuracies. We derive new tighter deterministic and probabilistic bounds that we use to verify a simulated (MPC) and a synthetic (LASSO) optimization problems solved on a reduced-precision machine in combination with an inaccurate proximal operator. We also show how the probabilistic bounds are more robust for algorithm verification and more accurate for application performance guarantees. Under some statistical assumptions, we also prove that some cumulative error terms follow a martingale property. And conforming to observations, e.g., in \cite{schmidt2011convergence}, we also show how the acceleration of the algorithm amplifies the gradient and proximal computational errors.

Image-Guided Depth Upsampling via Hessian and TV Priors

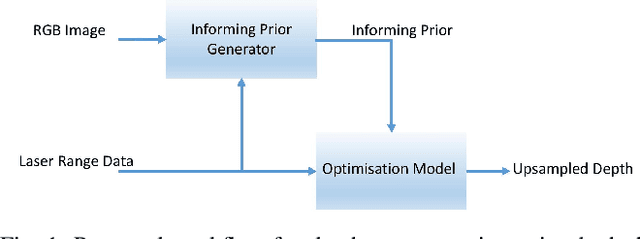
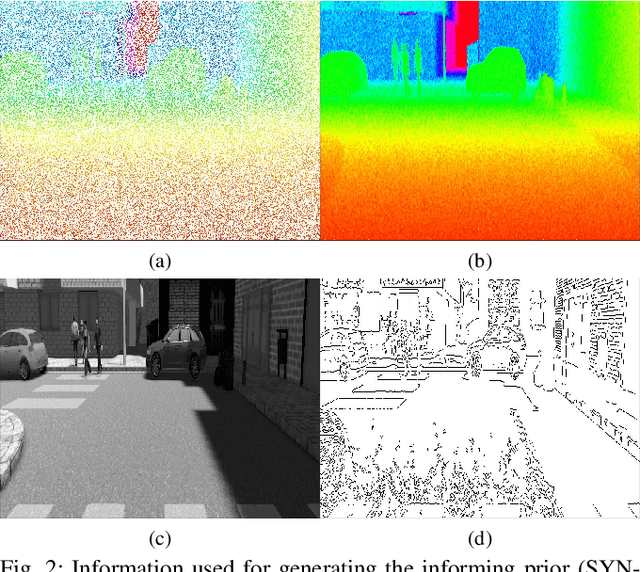
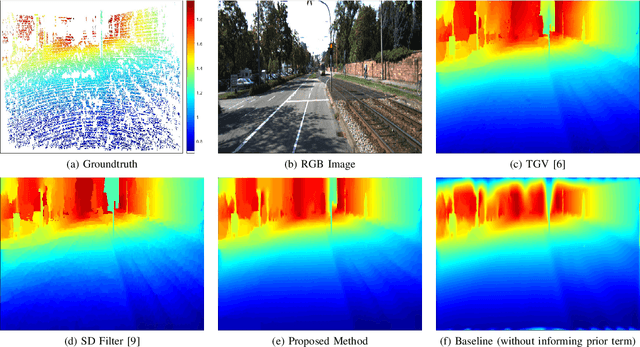
We propose a method that combines sparse depth (LiDAR) measurements with an intensity image and to produce a dense high-resolution depth image. As there are few, but accurate, depth measurements from the scene, our method infers the remaining depth values by incorporating information from the intensity image, namely the magnitudes and directions of the identified edges, and by assuming that the scene is composed mostly of flat surfaces. Such inference is achieved by solving a convex optimisation problem with properly weighted regularisers that are based on the `1-norm (specifically, on total variation). We solve the resulting problem with a computationally efficient ADMM-based algorithm. Using the SYNTHIA and KITTI datasets, our experiments show that the proposed method achieves a depth reconstruction performance comparable to or better than other model-based methods.