Efficient Dual-Blind Deconvolution for Joint Radar-Communication Systems Using ADMM: Enhancing Channel Estimation and Signal Recovery in 5G mmWave Networks

This paper introduces an innovative framework to address the dual-blind deconvolution challenge within joint radar-communication (JRC) systems, leveraging the Alternating Direction Method of Multipliers (ADMM) to estimate unknown radar channels G (or communication channel H) and transmitted signals X under convex constraints. The approach iteratively refines G (or H) and X estimates alongside auxiliary and dual variables, employing proximal operators to manage potential non-smoothness in the constraint functions. This method stands out for its computational efficiency and adaptability to a wide array of signal processing and communication problems where blind deconvolution is pivotal. Performance analysis reveals a notable reduction in communication mismatch and demonstrates significant improvements in key system metrics such as the Signal-to-Interference-plus-Noise Ratio (SINR), spectrum efficiency, and radar mutual information, particularly within the context of 5G millimeter-wave (mmWave) systems. These results underscore the proposed framework's potential to enhance the synergy between radar and communication functions, promoting more effective spectrum utilisation and environmental sensing capabilities in next-generation wireless technologies.

Context-Aware CSI Tracking and Path Loss Prediction Using Machine Learning and Dynamical Systems

In this paper, we present an advanced model for Channel State Information (CSI) tracking, leveraging a dynamical system approach to adapt CSI dynamically based on exogenous contextual information. This methodology allows for continuous updates to the Channel Knowledge Map (CKM), enhancing communication reliability and responsiveness in dynamic environments. To generate realistic and comprehensive datasets for training and evaluation, we developed a new MATLAB simulator that models radio wave propagation in urban environments. We address the challenge of real-time CKM adaptation using online learning of the Koopman operator, a technique that forecasts channel behaviour by exploiting dynamical system properties. Our approach supports real-time updates with high accuracy and efficiency, as demonstrated by experiments with varying window sizes for the Koopman Autoencoder model. A window size of 100 was found to offer the best balance between prediction accuracy (RMSE: 1.8323 +- 1.1071, MAE: 0.3780 +- 0.2221) and computational efficiency (training time: 231.1 +- 82.5 ms, prediction time: 109.0 +- 55.7 ms). Additionally, we introduce a moving window mechanism to address privacy and security concerns by updating the Koopman operator within the window and purging input data thereafter, minimising data retention and storage risks. This ensures the CKM remains accurate and relevant while maintaining stringent data privacy standards. Our findings suggest that this approach can significantly improve the resilience and security of communication systems, making them highly adaptable to environmental changes without compromising user privacy.

Trade-offs in Reliability and Performance Using Selective Beamforming for Ultra-Massive MIMO

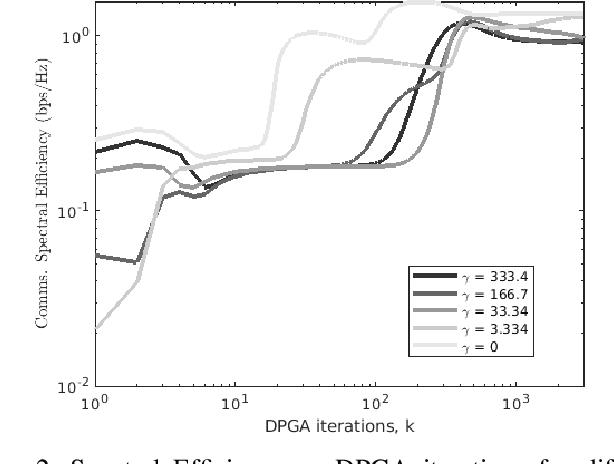
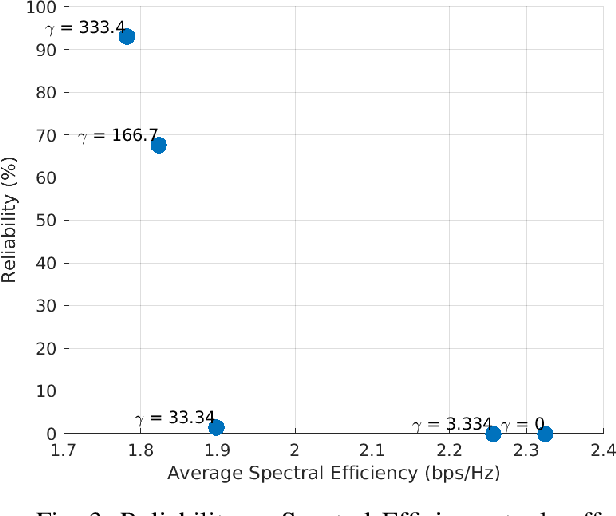
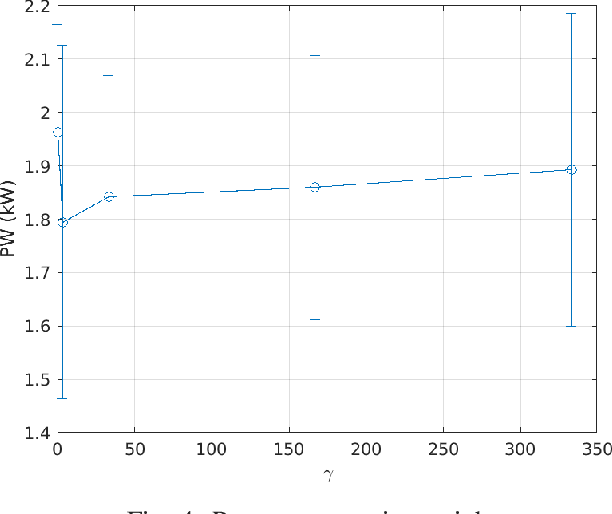
This paper addresses the optimisation challenges in Ultra-Massive MIMO communication systems, focusing on array selection and beamforming in dynamic and diverse operational contexts. We introduce a novel array selection criterion that incorporates antenna health information into the optimisation process, distinguishing our approach from traditional methods. Our methodology employs dual proximal-gradient ascent to effectively tackle the constrained non-convex and non-smooth nature of sparse array selection problems. A central feature of our strategy is the implementation of proportional fairness among communication users, aligning with system resource limitations while ensuring minimum rate requirements for all users. This approach not only enhances system efficiency and responsiveness but also ensures equitable resource distribution. Extensive simulations validate the effectiveness of the proposed solutions in optimising Ultra-Massive MIMO system performance, demonstrating their applicability in complex communication scenarios. Our findings reveal key trade-offs influenced by the sparsity promotion weight ({\gamma}). As {\gamma} increases, spectral efficiency (SE) and communication rate (Ri) decrease, while beamforming matrix density (BMD) reduces and antenna reliability (RL) significantly improves. These results highlight the critical balance between performance and reliability, essential for the practical deployment of Ultra-Massive MIMO systems. This work advances the field by providing innovative solutions and new insights into array selection and beamforming optimization, setting a foundation for future research in Ultra-Massive MIMO communication systems.

Reconfigurable FPGA-Based Solvers For Sparse Satellite Control

This paper introduces a novel reconfigurable and power-efficient FPGA (Field-Programmable Gate Array) implementation of an operator splitting algorithm for Non-Terrestial Network's (NTN) relay satellites model predictive orientation control (MPC). Our approach ensures system stability and introduces an innovative reconfigurable bit-width FPGA-based optimization solver. To demonstrate its efficacy, we employ a real FPGA-In-the-Loop hardware setup to control simulated satellite dynamics. Furthermore, we conduct an in-depth comparative analysis, examining various fixed-point configurations to evaluate the combined system's closed-loop performance and power efficiency, providing a holistic understanding of the proposed implementation's advantages.

Improved Convergence Bounds For Operator Splitting Algorithms With Rare Extreme Errors

In this paper, we improve upon our previous work[24,22] and establish convergence bounds on the objective function values of approximate proximal-gradient descent (AxPGD), approximate accelerated proximal-gradient descent (AxAPGD) and approximate proximal ADMM (AxWLM-ADMM) schemes. We consider approximation errors that manifest rare extreme events and we propagate their effects through iterations. We establish probabilistic asymptotic and non-asymptotic convergence bounds as functions of the range (upper/lower bounds) and variance of approximation errors. We use the derived bound to assess AxPGD in a sparse model predictive control of a spacecraft system and compare its accuracy with previously derived bounds.

A Low-Power Hardware-Friendly Optimisation Algorithm With Absolute Numerical Stability and Convergence Guarantees

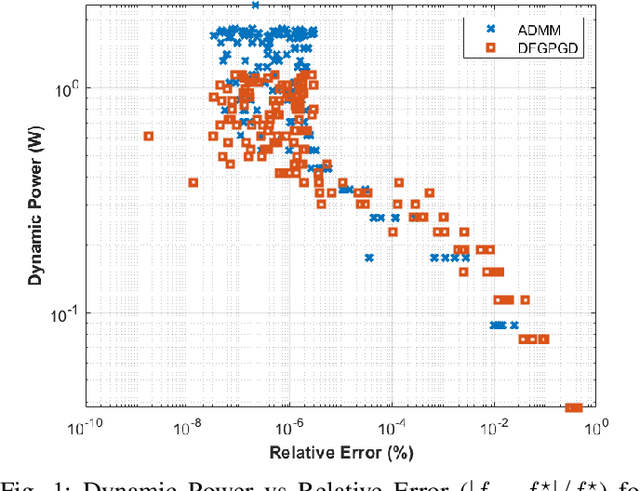
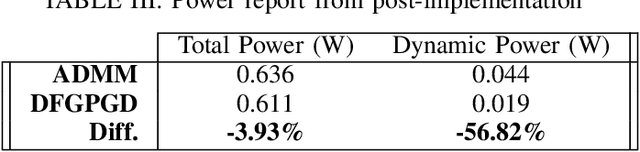
We propose Dual-Feedback Generalized Proximal Gradient Descent (DFGPGD) as a new, hardware-friendly, operator splitting algorithm. We then establish convergence guarantees under approximate computational errors and we derive theoretical criteria for the numerical stability of DFGPGD based on absolute stability of dynamical systems. We also propose a new generalized proximal ADMM that can be used to instantiate most of existing proximal-based composite optimization solvers. We implement DFGPGD and ADMM on FPGA ZCU106 board and compare them in light of FPGA's timing as well as resource utilization and power efficiency. We also perform a full-stack, application-to-hardware, comparison between approximate versions of DFGPGD and ADMM based on dynamic power/error rate trade-off, which is a new hardware-application combined metric.

Probabilistic Verification of Approximate Algorithms with Unstructured Errors: Application to Fully Inexact Generalized ADMM

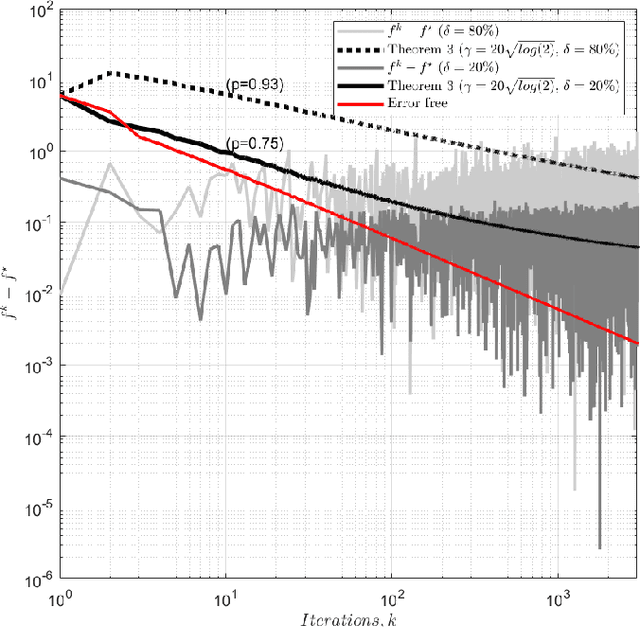
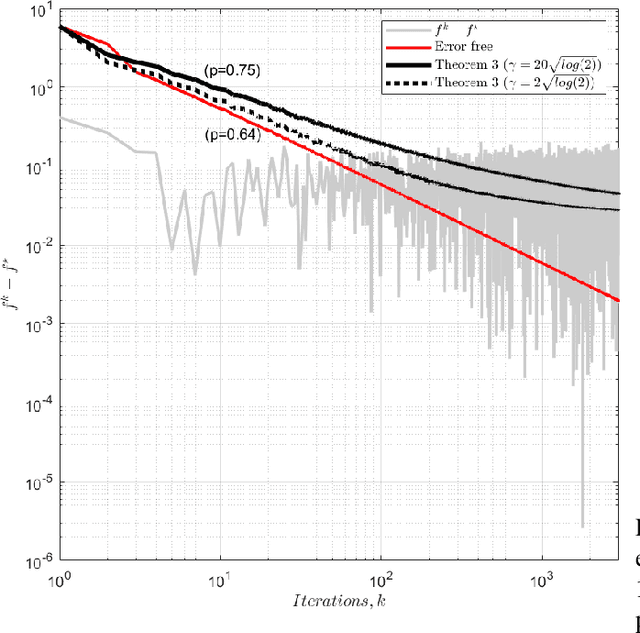
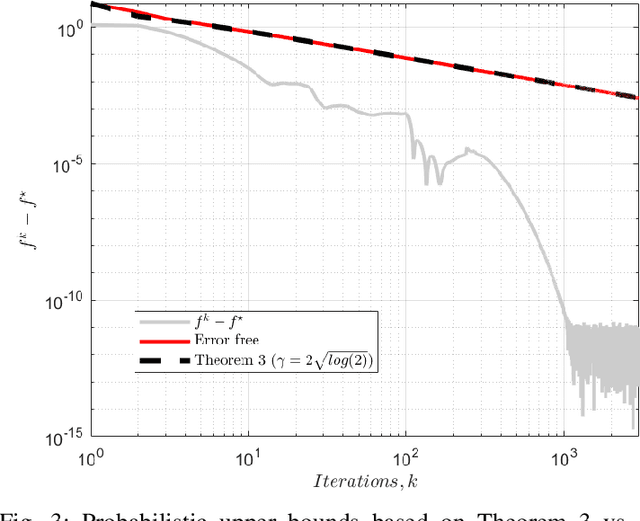
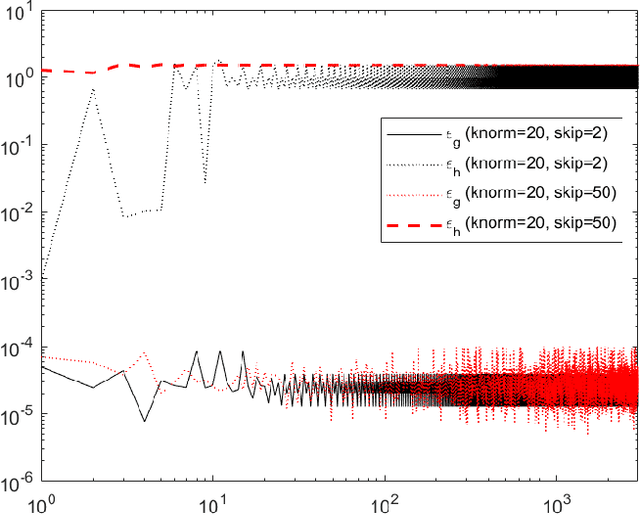
We analyse the convergence of an approximate, fully inexact, ADMM algorithm under additive, deterministic and probabilistic error models. We consider the generalized ADMM scheme that is derived from generalized Lagrangian penalty with additive (smoothing) adaptive-metric quadratic proximal perturbations. We derive explicit deterministic and probabilistic convergence upper bounds for the lower-C2 nonconvex case as well as the convex case under the Lipschitz continuity condition. We also present more practical conditions on the proximal errors under which convergence of the approximate ADMM to a suboptimal solution is guaranteed with high probability. We consider statistically and dynamically-unstructured conditional mean independent bounded error sequences. We validate our results using both simulated and practical software and algorithmic computational perturbations. We apply the proposed algorithm to a synthetic LASSO and robust regression with k-support norm regularization problems and test our proposed bounds under different computational noise levels. Compared to classical convergence results, the adaptive probabilistic bounds are more accurate in predicting the distance from the optimal set and parasitic residual error under different sources of inaccuracies.

Sharper Bounds for Proximal Gradient Algorithms with Errors

We analyse the convergence of the proximal gradient algorithm for convex composite problems in the presence of gradient and proximal computational inaccuracies. We derive new tighter deterministic and probabilistic bounds that we use to verify a simulated (MPC) and a synthetic (LASSO) optimization problems solved on a reduced-precision machine in combination with an inaccurate proximal operator. We also show how the probabilistic bounds are more robust for algorithm verification and more accurate for application performance guarantees. Under some statistical assumptions, we also prove that some cumulative error terms follow a martingale property. And conforming to observations, e.g., in \cite{schmidt2011convergence}, we also show how the acceleration of the algorithm amplifies the gradient and proximal computational errors.