Probabilistic Verification of Approximate Algorithms with Unstructured Errors: Application to Fully Inexact Generalized ADMM
Paper and Code
Oct 05, 2022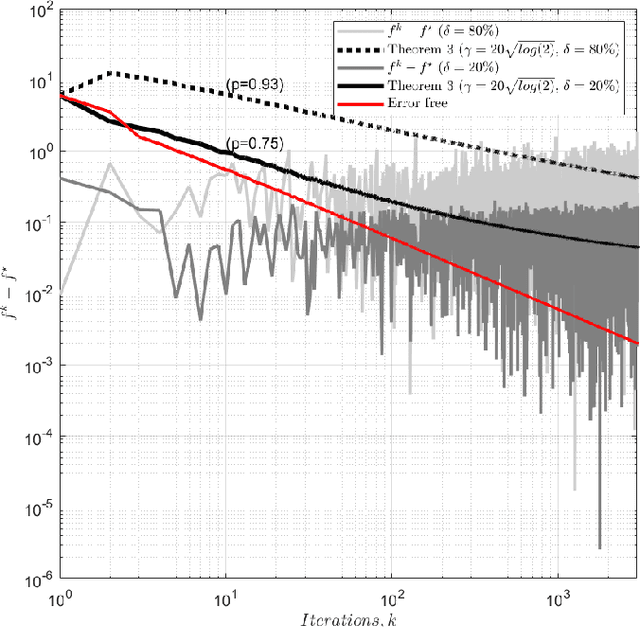
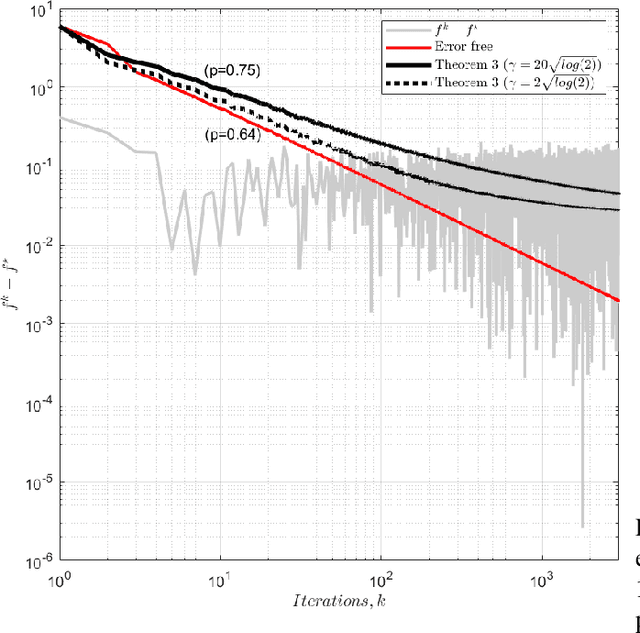
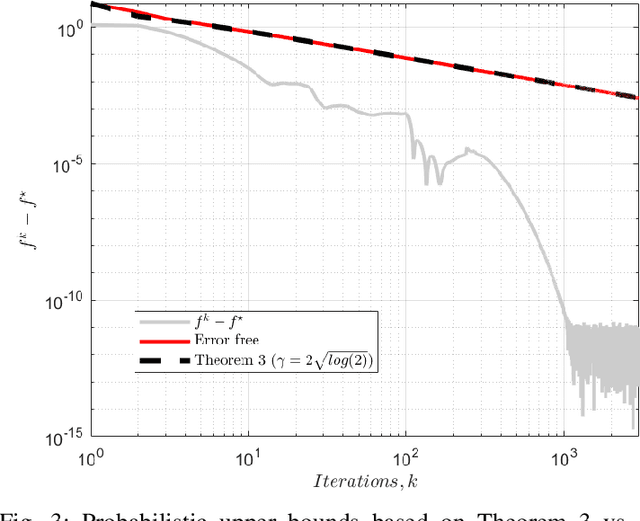
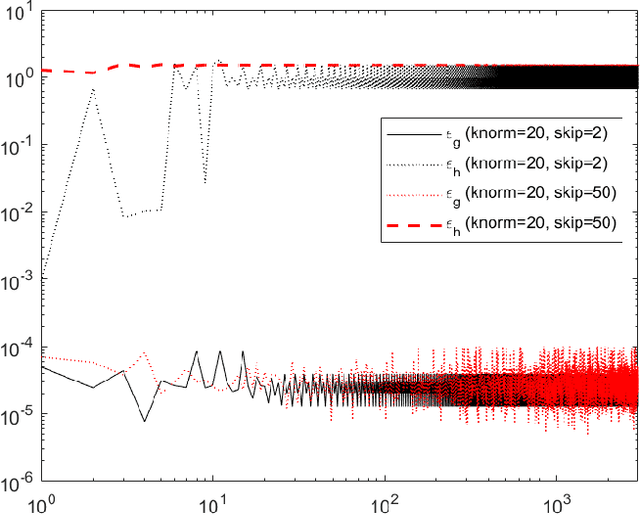
We analyse the convergence of an approximate, fully inexact, ADMM algorithm under additive, deterministic and probabilistic error models. We consider the generalized ADMM scheme that is derived from generalized Lagrangian penalty with additive (smoothing) adaptive-metric quadratic proximal perturbations. We derive explicit deterministic and probabilistic convergence upper bounds for the lower-C2 nonconvex case as well as the convex case under the Lipschitz continuity condition. We also present more practical conditions on the proximal errors under which convergence of the approximate ADMM to a suboptimal solution is guaranteed with high probability. We consider statistically and dynamically-unstructured conditional mean independent bounded error sequences. We validate our results using both simulated and practical software and algorithmic computational perturbations. We apply the proposed algorithm to a synthetic LASSO and robust regression with k-support norm regularization problems and test our proposed bounds under different computational noise levels. Compared to classical convergence results, the adaptive probabilistic bounds are more accurate in predicting the distance from the optimal set and parasitic residual error under different sources of inaccuracies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge