A Low-Power Hardware-Friendly Optimisation Algorithm With Absolute Numerical Stability and Convergence Guarantees
Paper and Code
Jun 29, 2023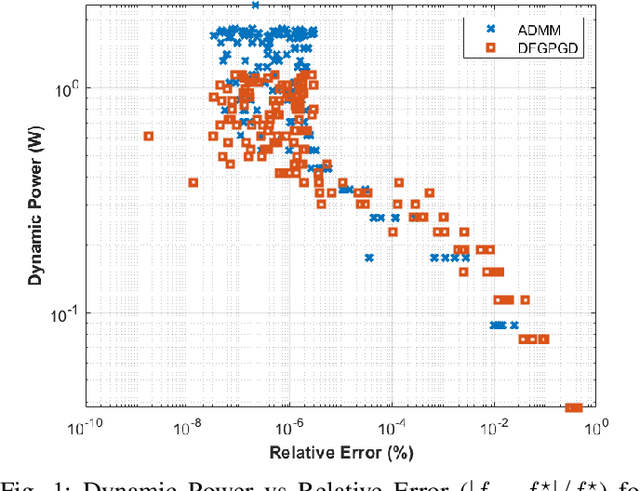

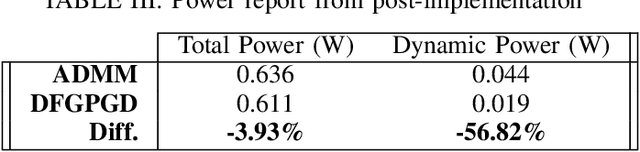
We propose Dual-Feedback Generalized Proximal Gradient Descent (DFGPGD) as a new, hardware-friendly, operator splitting algorithm. We then establish convergence guarantees under approximate computational errors and we derive theoretical criteria for the numerical stability of DFGPGD based on absolute stability of dynamical systems. We also propose a new generalized proximal ADMM that can be used to instantiate most of existing proximal-based composite optimization solvers. We implement DFGPGD and ADMM on FPGA ZCU106 board and compare them in light of FPGA's timing as well as resource utilization and power efficiency. We also perform a full-stack, application-to-hardware, comparison between approximate versions of DFGPGD and ADMM based on dynamic power/error rate trade-off, which is a new hardware-application combined metric.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge