A Stochastic Composite Augmented Lagrangian Method For Reinforcement Learning

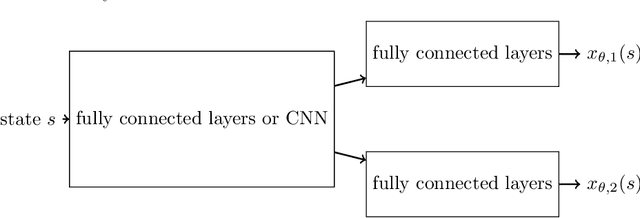
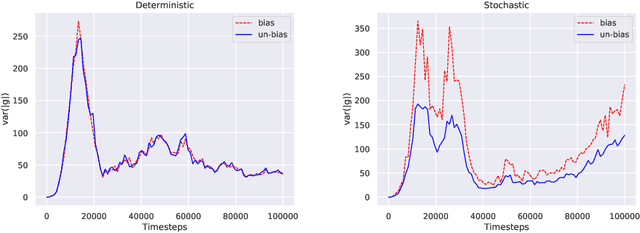
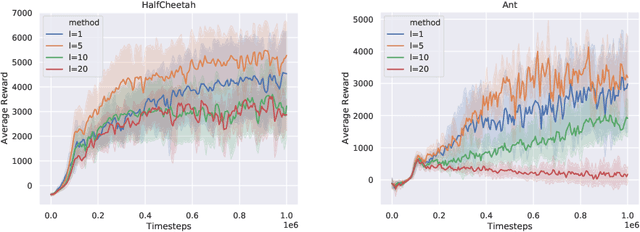
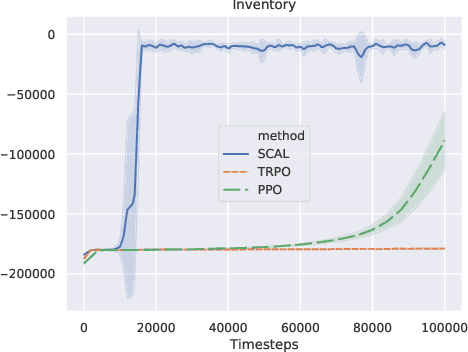
In this paper, we consider the linear programming (LP) formulation for deep reinforcement learning. The number of the constraints depends on the size of state and action spaces, which makes the problem intractable in large or continuous environments. The general augmented Lagrangian method suffers the double-sampling obstacle in solving the LP. Namely, the conditional expectations originated from the constraint functions and the quadratic penalties in the augmented Lagrangian function impose difficulties in sampling and evaluation. Motivated from the updates of the multipliers, we overcome the obstacles in minimizing the augmented Lagrangian function by replacing the intractable conditional expectations with the multipliers. Therefore, a deep parameterized augment Lagrangian method is proposed. Furthermore, the replacement provides a promising breakthrough to integrate the two steps in the augmented Lagrangian method into a single constrained problem. A general theoretical analysis shows that the solutions generated from a sequence of the constrained optimizations converge to the optimal solution of the LP if the error is controlled properly. A theoretical analysis on the quadratic penalty algorithm under neural tangent kernel setting shows the residual can be arbitrarily small if the parameter in network and optimization algorithm is chosen suitably. Preliminary experiments illustrate that our method is competitive to other state-of-the-art algorithms.

Structured Stochastic Quasi-Newton Methods for Large-Scale Optimization Problems

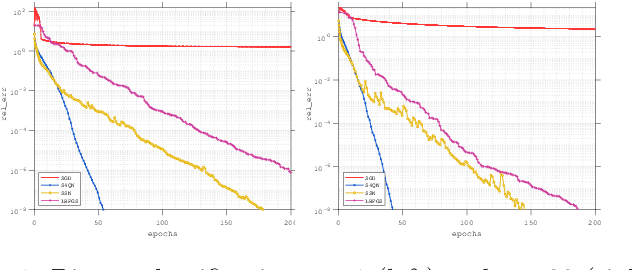
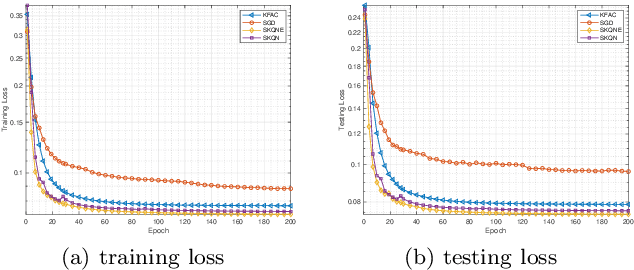
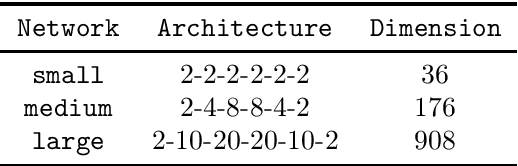
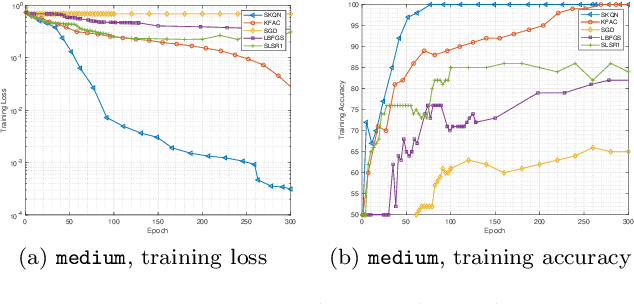
In this paper, we consider large-scale finite-sum nonconvex problems arising from machine learning. Since the Hessian is often a summation of a relative cheap and accessible part and an expensive or even inaccessible part, a stochastic quasi-Newton matrix is constructed using partial Hessian information as much as possible. By further exploiting the low-rank structures based on the Nystr\"om approximation, the computation of the quasi-Newton direction is affordable. To make full use of the gradient estimation, we also develop an extra-step strategy for this framework. Global convergence to stationary point in expectation and local suplinear convergence rate are established under some mild assumptions. Numerical experiments on logistic regression, deep autoencoder networks and deep learning problems show that the efficiency of our proposed method is at least comparable with the state-of-the-art methods.

Sketchy Empirical Natural Gradient Methods for Deep Learning

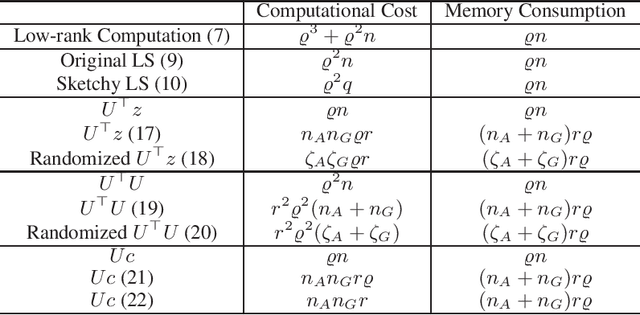
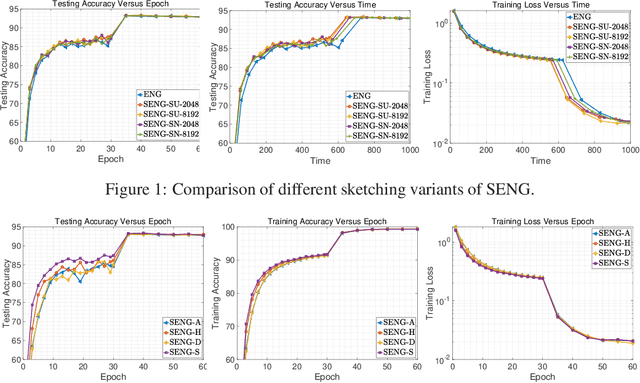
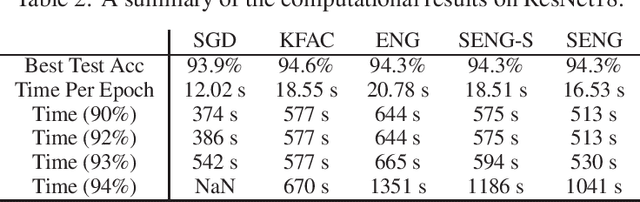
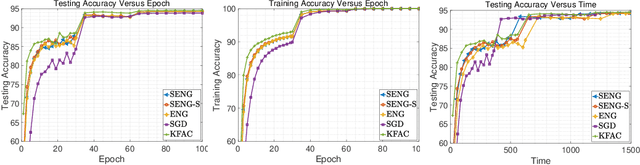
In this paper, we develop an efficient sketchy empirical natural gradient method for large-scale finite-sum optimization problems from deep learning. The empirical Fisher information matrix is usually low-rank since the sampling is only practical on a small amount of data at each iteration. Although the corresponding natural gradient direction lies in a small subspace, both the computational cost and memory requirement are still not tractable due to the curse of dimensionality. We design randomized techniques for different neural network structures to resolve these challenges. For layers with a reasonable dimension, a sketching can be performed on a regularized least squares subproblem. Otherwise, since the gradient is a vectorization of the product between two matrices, we apply sketching on low-rank approximation of these matrices to compute the most expensive parts. Global convergence to stationary point is established under some mild assumptions. Numerical results on deep convolution networks illustrate that our method is quite competitive to the state-of-the-art methods such as SGD and KFAC.