Sketchy Empirical Natural Gradient Methods for Deep Learning

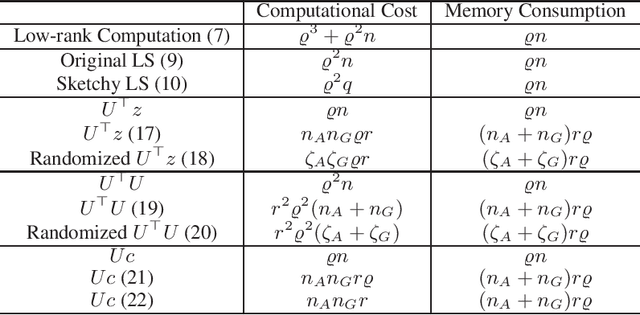
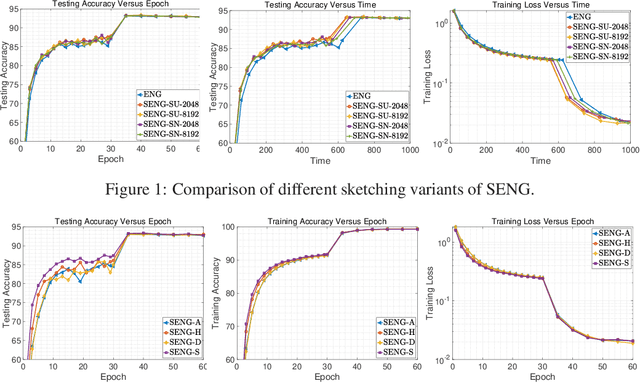
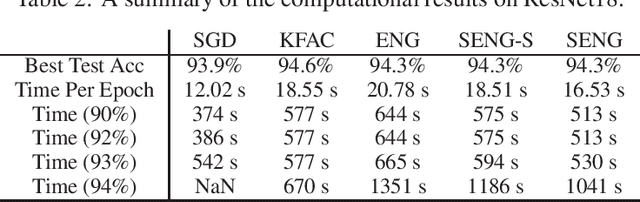
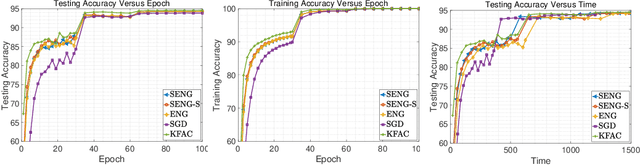
In this paper, we develop an efficient sketchy empirical natural gradient method for large-scale finite-sum optimization problems from deep learning. The empirical Fisher information matrix is usually low-rank since the sampling is only practical on a small amount of data at each iteration. Although the corresponding natural gradient direction lies in a small subspace, both the computational cost and memory requirement are still not tractable due to the curse of dimensionality. We design randomized techniques for different neural network structures to resolve these challenges. For layers with a reasonable dimension, a sketching can be performed on a regularized least squares subproblem. Otherwise, since the gradient is a vectorization of the product between two matrices, we apply sketching on low-rank approximation of these matrices to compute the most expensive parts. Global convergence to stationary point is established under some mild assumptions. Numerical results on deep convolution networks illustrate that our method is quite competitive to the state-of-the-art methods such as SGD and KFAC.