Structured Stochastic Quasi-Newton Methods for Large-Scale Optimization Problems
Paper and Code
Jun 17, 2020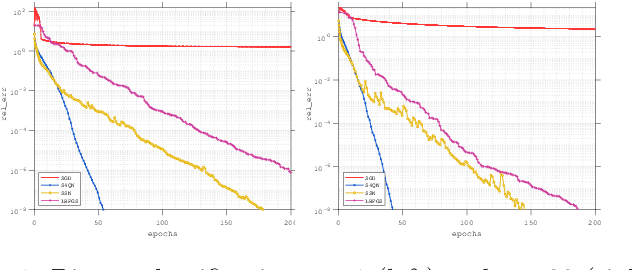
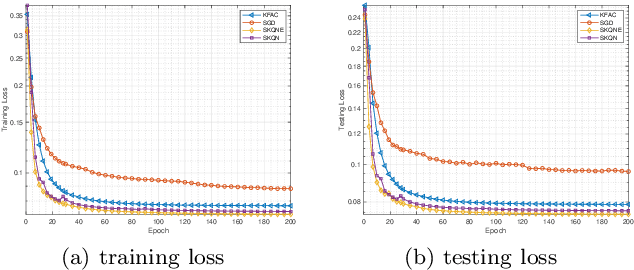
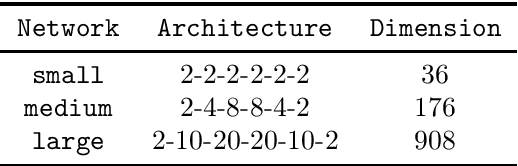
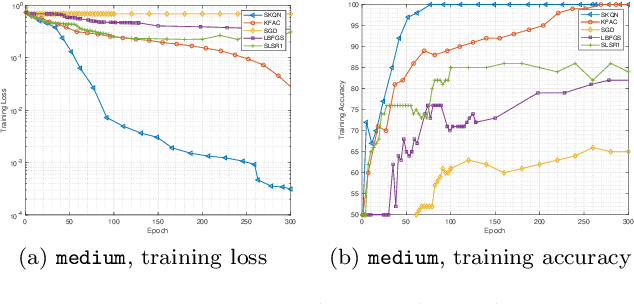
In this paper, we consider large-scale finite-sum nonconvex problems arising from machine learning. Since the Hessian is often a summation of a relative cheap and accessible part and an expensive or even inaccessible part, a stochastic quasi-Newton matrix is constructed using partial Hessian information as much as possible. By further exploiting the low-rank structures based on the Nystr\"om approximation, the computation of the quasi-Newton direction is affordable. To make full use of the gradient estimation, we also develop an extra-step strategy for this framework. Global convergence to stationary point in expectation and local suplinear convergence rate are established under some mild assumptions. Numerical experiments on logistic regression, deep autoencoder networks and deep learning problems show that the efficiency of our proposed method is at least comparable with the state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge