A Stochastic Composite Augmented Lagrangian Method For Reinforcement Learning
Paper and Code
May 20, 2021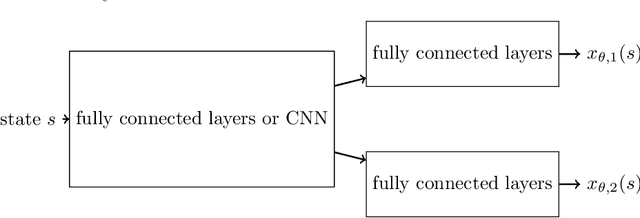
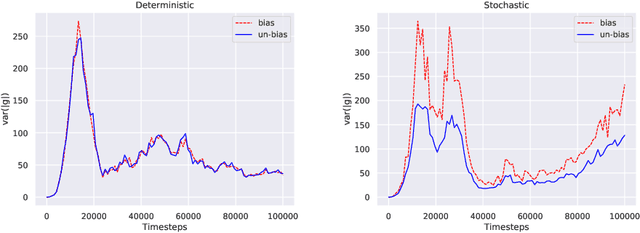
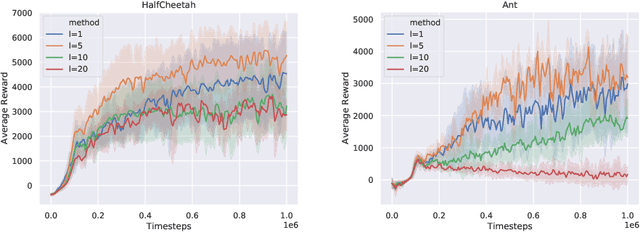
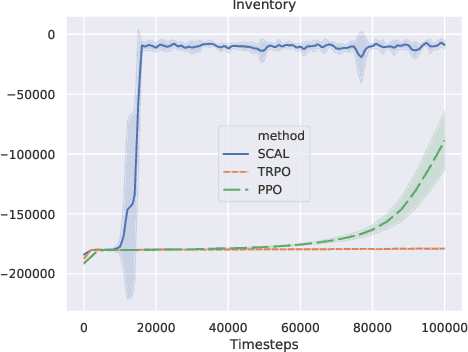
In this paper, we consider the linear programming (LP) formulation for deep reinforcement learning. The number of the constraints depends on the size of state and action spaces, which makes the problem intractable in large or continuous environments. The general augmented Lagrangian method suffers the double-sampling obstacle in solving the LP. Namely, the conditional expectations originated from the constraint functions and the quadratic penalties in the augmented Lagrangian function impose difficulties in sampling and evaluation. Motivated from the updates of the multipliers, we overcome the obstacles in minimizing the augmented Lagrangian function by replacing the intractable conditional expectations with the multipliers. Therefore, a deep parameterized augment Lagrangian method is proposed. Furthermore, the replacement provides a promising breakthrough to integrate the two steps in the augmented Lagrangian method into a single constrained problem. A general theoretical analysis shows that the solutions generated from a sequence of the constrained optimizations converge to the optimal solution of the LP if the error is controlled properly. A theoretical analysis on the quadratic penalty algorithm under neural tangent kernel setting shows the residual can be arbitrarily small if the parameter in network and optimization algorithm is chosen suitably. Preliminary experiments illustrate that our method is competitive to other state-of-the-art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge