Can GPT tell us why these images are synthesized? Empowering Multimodal Large Language Models for Forensics

The rapid development of generative AI facilitates content creation and makes image manipulation easier and more difficult to detect. While multimodal Large Language Models (LLMs) have encoded rich world knowledge, they are not inherently tailored for combating AI-generated Content (AIGC) and struggle to comprehend local forgery details. In this work, we investigate the application of multimodal LLMs in forgery detection. We propose a framework capable of evaluating image authenticity, localizing tampered regions, providing evidence, and tracing generation methods based on semantic tampering clues. Our method demonstrates that the potential of LLMs in forgery analysis can be effectively unlocked through meticulous prompt engineering and the application of few-shot learning techniques. We conduct qualitative and quantitative experiments and show that GPT4V can achieve an accuracy of 92.1% in Autosplice and 86.3% in LaMa, which is competitive with state-of-the-art AIGC detection methods. We further discuss the limitations of multimodal LLMs in such tasks and propose potential improvements.

Detecting Low Pass Graph Signals via Spectral Pattern: Sampling Complexity and Applications

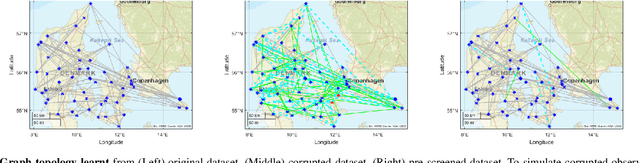
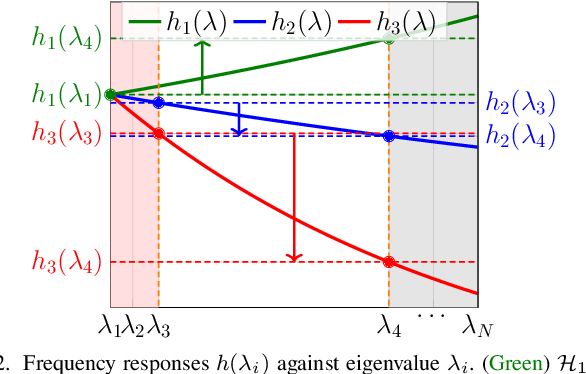
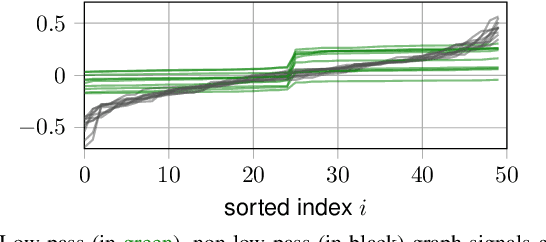
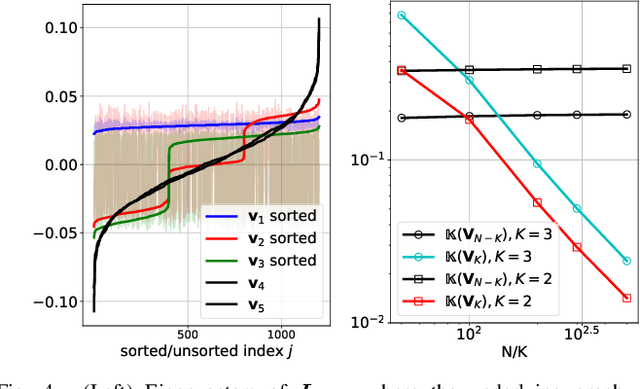
This paper proposes a blind detection problem for low pass graph signals. Without assuming knowledge of the graph topology in advance, we aim to detect if a set of graph signal observations are generated from a low pass graph filter. Our problem is motivated by the widely adopted assumption of low pass (a.k.a.~smooth) signals required by many existing works in graph signal processing (GSP), as well as the longstanding problem of network dynamics identification. Focusing on detecting low pass graph signals whose cutoff frequency coincides with the number of clusters present, our key idea is to develop blind detector leveraging the unique spectral pattern exhibited by low pass graph signals. We analyze the sample complexity of these detectors considering the effects of graph filter's properties, random delays. We show novel applications of the blind detector on robustifying graph learning, identifying antagonistic ties in opinion dynamics, and detecting anomalies in power systems. Numerical experiments validate our findings.

Product Graph Learning from Multi-attribute Graph Signals with Inter-layer Coupling

This paper considers learning a product graph from multi-attribute graph signals. Our work is motivated by the widespread presence of multilayer networks that feature interactions within and across graph layers. Focusing on a product graph setting with homogeneous layers, we propose a bivariate polynomial graph filter model. We then consider the topology inference problems thru adapting existing spectral methods. We propose two solutions for the required spectral estimation step: a simplified solution via unfolding the multi-attribute data into matrices, and an exact solution via nearest Kronecker product decomposition (NKD). Interestingly, we show that strong inter-layer coupling can degrade the performance of the unfolding solution while the NKD solution is robust to inter-layer coupling effects. Numerical experiments show efficacy of our methods.

Online Inference for Mixture Model of Streaming Graph Signals with Non-White Excitation

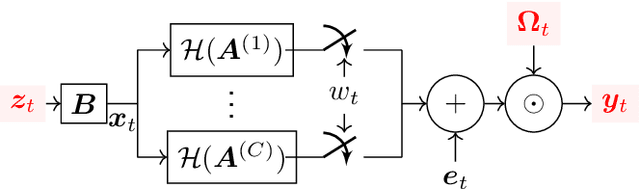
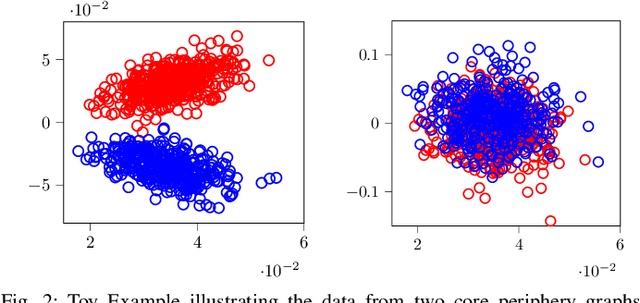
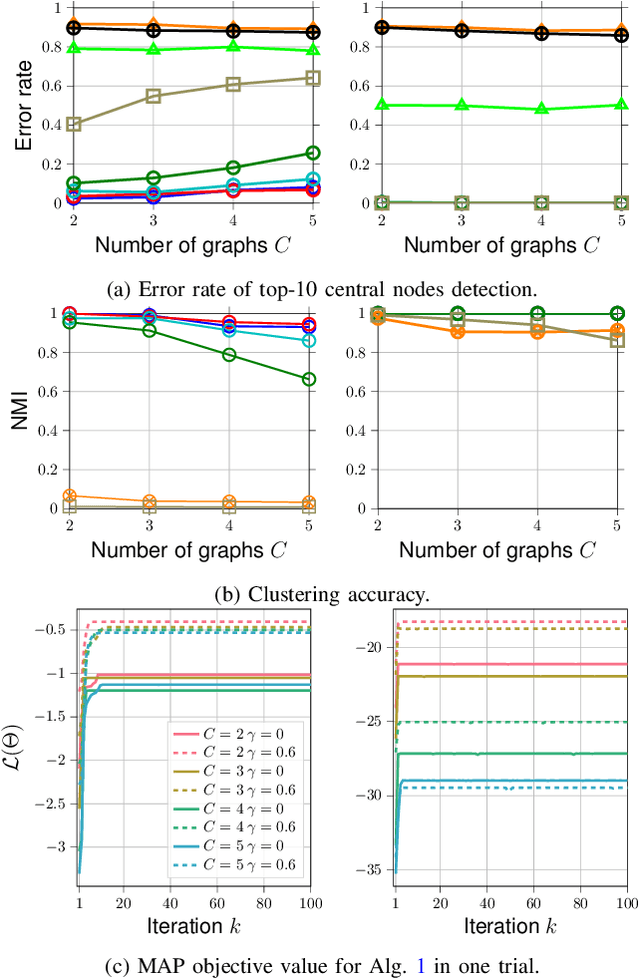
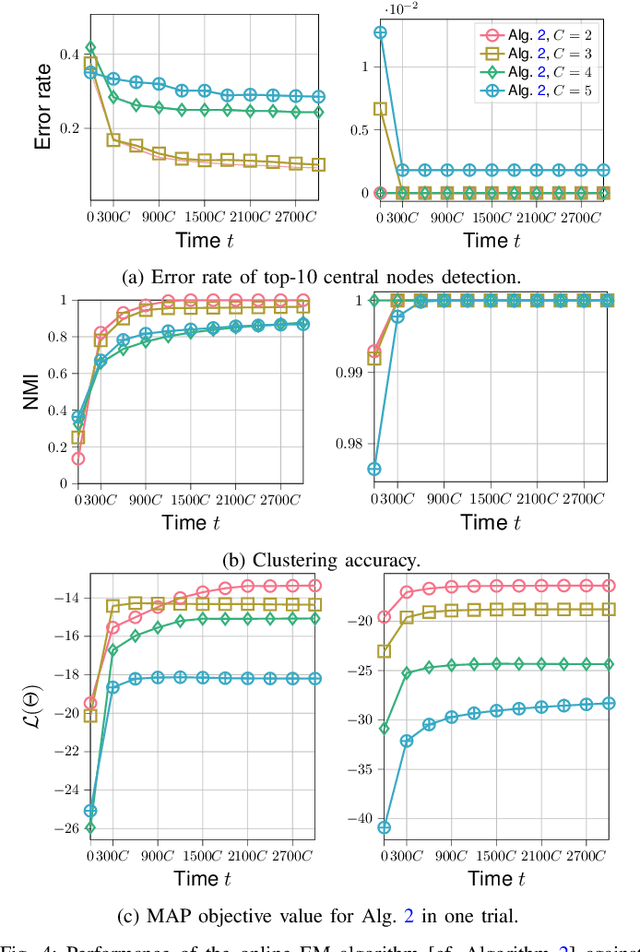
This paper considers a joint multi-graph inference and clustering problem for simultaneous inference of node centrality and association of graph signals with their graphs. We study a mixture model of filtered low pass graph signals with possibly non-white and low-rank excitation. While the mixture model is motivated from practical scenarios, it presents significant challenges to prior graph learning methods. As a remedy, we consider an inference problem focusing on the node centrality of graphs. We design an expectation-maximization (EM) algorithm with a unique low-rank plus sparse prior derived from low pass signal property. We propose a novel online EM algorithm for inference from streaming data. As an example, we extend the online algorithm to detect if the signals are generated from an abnormal graph. We show that the proposed algorithms converge to a stationary point of the maximum-a-posterior (MAP) problem. Numerical experiments support our analysis.

On the Stability of Low Pass Graph Filter With a Large Number of Edge Rewires

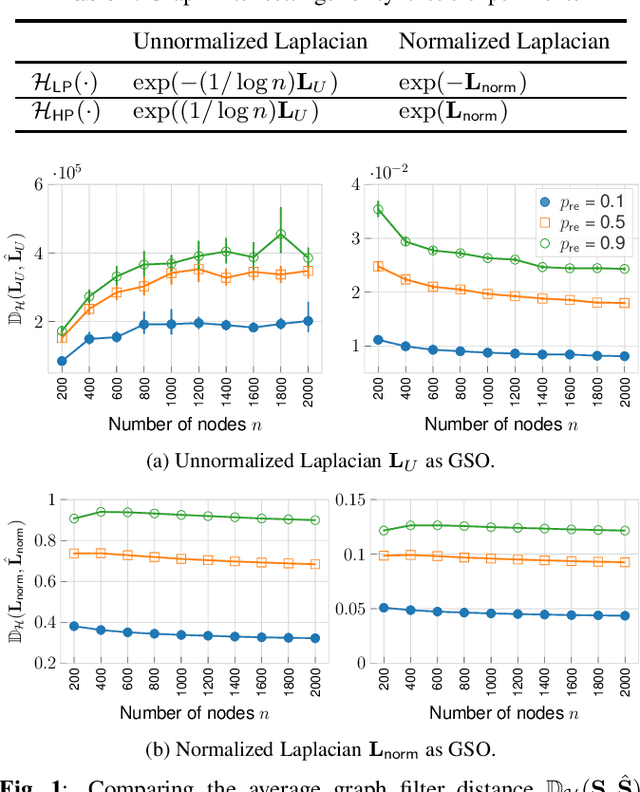
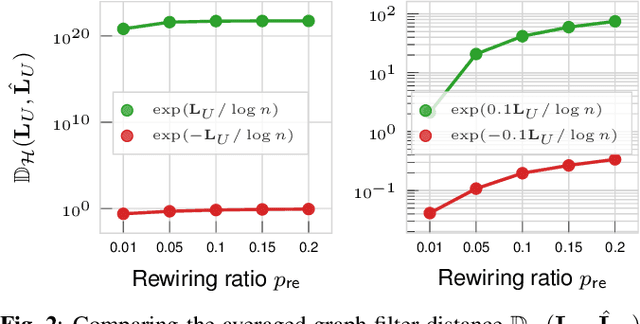
Recently, the stability of graph filters has been studied as one of the key theoretical properties driving the highly successful graph convolutional neural networks (GCNs). The stability of a graph filter characterizes the effect of topology perturbation on the output of a graph filter, a fundamental building block for GCNs. Many existing results have focused on the regime of small perturbation with a small number of edge rewires. However, the number of edge rewires can be large in many applications. To study the latter case, this work departs from the previous analysis and proves a bound on the stability of graph filter relying on the filter's frequency response. Assuming the graph filter is low pass, we show that the stability of the filter depends on perturbation to the community structure. As an application, we show that for stochastic block model graphs, the graph filter distance converges to zero when the number of nodes approaches infinity. Numerical simulations validate our findings.

Detecting Central Nodes from Low-rank Excited Graph Signals via Structured Factor Analysis

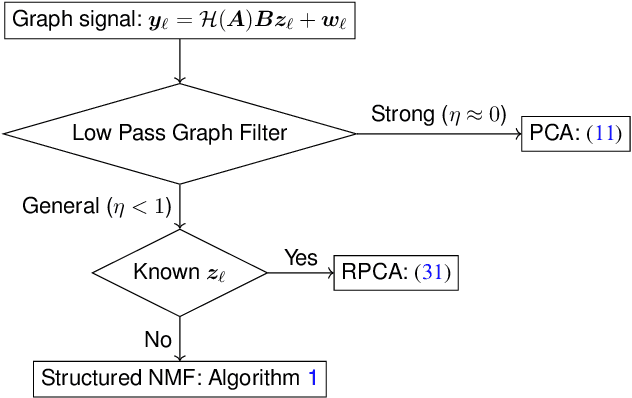
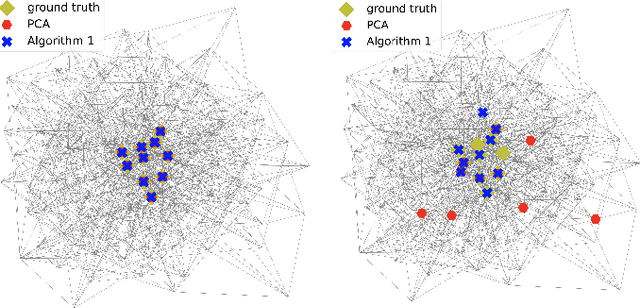
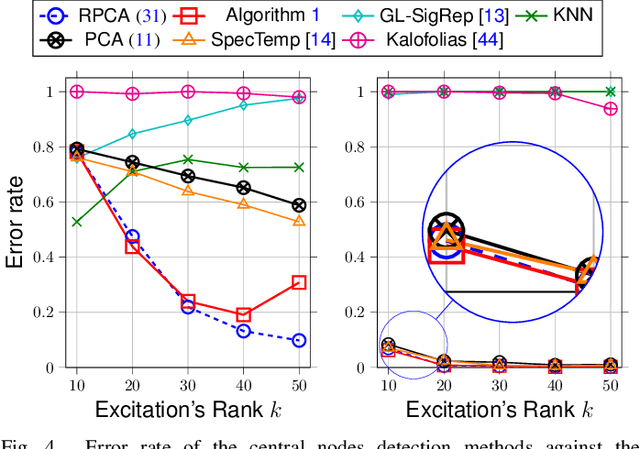
This paper treats a blind detection problem to identify the central nodes in a graph from filtered graph signals. Unlike prior works which impose strong restrictions on the data model, we only require the underlying graph filter to satisfy a low pass property with a generic low-rank excitation model. We treat two cases depending on the low pass graph filter's strength. When the graph filter is strong low pass, i.e., it has a frequency response that drops sharply at the high frequencies, we show that the principal component analysis (PCA) method detects central nodes with high accuracy. For general low pass graph filter, we show that the graph signals can be described by a structured factor model featuring the product between a low-rank plus sparse factor and an unstructured factor. We propose a two-stage decomposition algorithm to learn the structured factor model via a judicious combination of the non-negative matrix factorization and robust PCA algorithms. We analyze the identifiability conditions for the model which lead to accurate central nodes detection. Numerical experiments on synthetic and real data are provided to support our findings. We demonstrate significant performance gains over prior works.

Identifying First-order Lowpass Graph Signals using Perron Frobenius Theorem

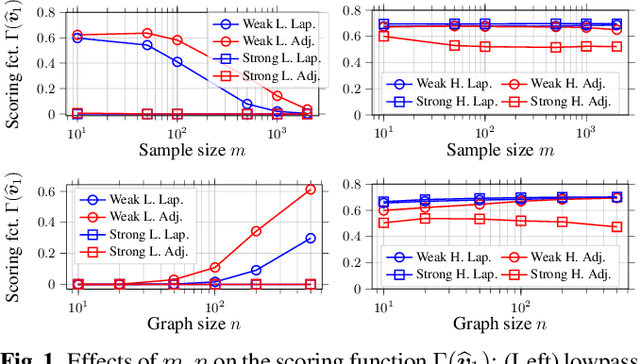
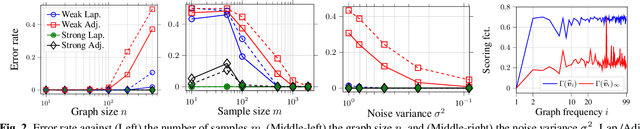
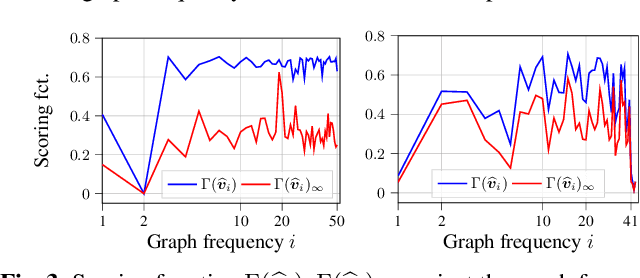
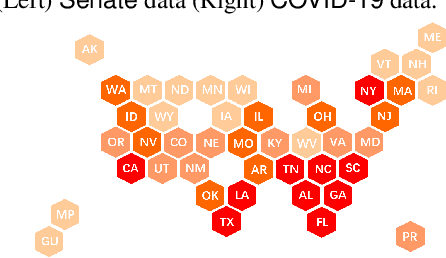
This paper is concerned with the blind identification of graph filters from graph signals. Our aim is to determine if the graph filter generating the graph signals is first-order lowpass without knowing the graph topology. Notice that lowpass graph filter is a common prerequisite for applying graph signal processing tools for sampling, denoising, and graph learning. Our method is inspired by the Perron Frobenius theorem, which observes that for first-order lowpass graph filter, the top eigenvector of output covariance would be the only eigenvector with elements of the same sign. Utilizing this observation, we develop a simple detector that answers if a given data set is produced by a first-order lowpass graph filter. We analyze the effects of finite-sample, graph size, observation noise, strength of lowpass filter, on the detector's performance. Numerical experiments on synthetic and real data support our findings.