Detecting Low Pass Graph Signals via Spectral Pattern: Sampling Complexity and Applications

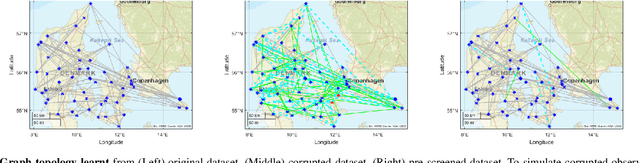
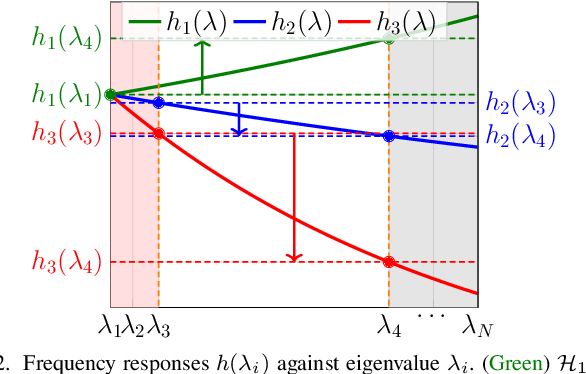
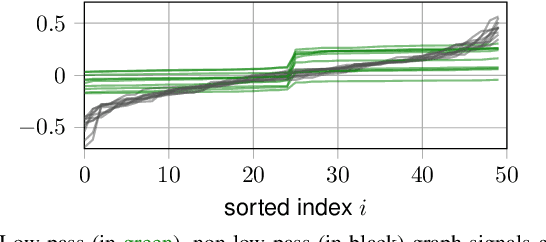
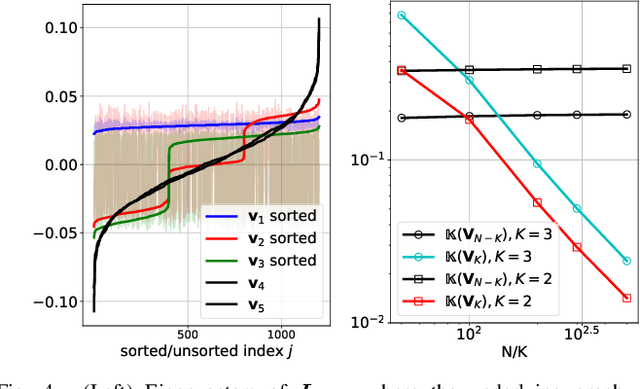
This paper proposes a blind detection problem for low pass graph signals. Without assuming knowledge of the graph topology in advance, we aim to detect if a set of graph signal observations are generated from a low pass graph filter. Our problem is motivated by the widely adopted assumption of low pass (a.k.a.~smooth) signals required by many existing works in graph signal processing (GSP), as well as the longstanding problem of network dynamics identification. Focusing on detecting low pass graph signals whose cutoff frequency coincides with the number of clusters present, our key idea is to develop blind detector leveraging the unique spectral pattern exhibited by low pass graph signals. We analyze the sample complexity of these detectors considering the effects of graph filter's properties, random delays. We show novel applications of the blind detector on robustifying graph learning, identifying antagonistic ties in opinion dynamics, and detecting anomalies in power systems. Numerical experiments validate our findings.