Detecting Central Nodes from Low-rank Excited Graph Signals via Structured Factor Analysis
Paper and Code
Sep 28, 2021
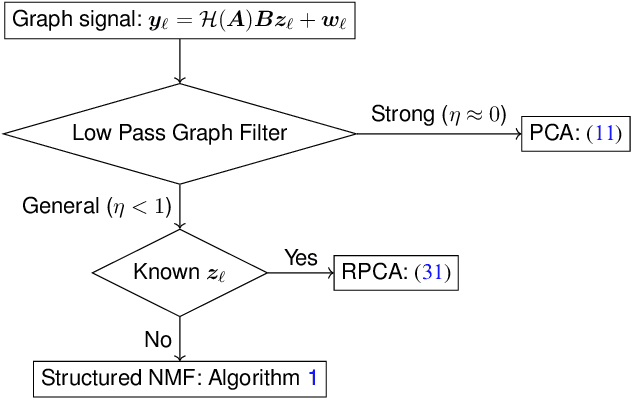
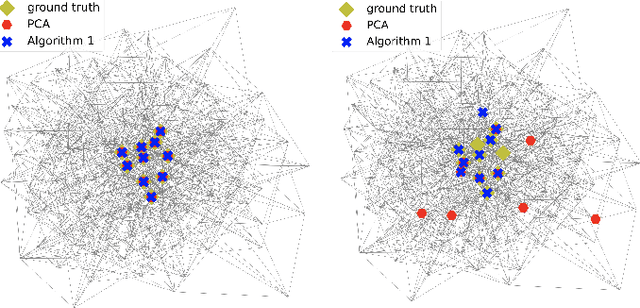
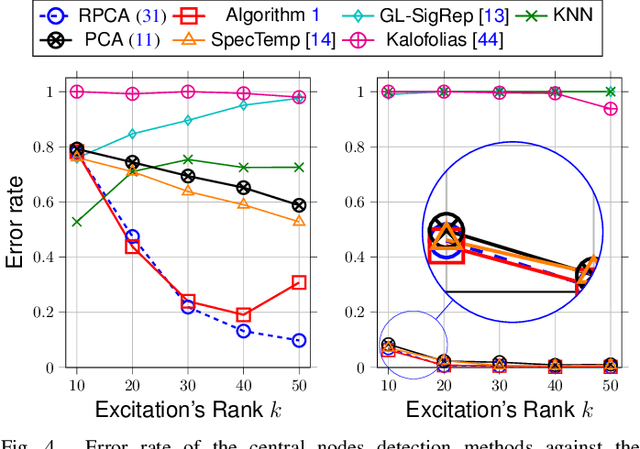
This paper treats a blind detection problem to identify the central nodes in a graph from filtered graph signals. Unlike prior works which impose strong restrictions on the data model, we only require the underlying graph filter to satisfy a low pass property with a generic low-rank excitation model. We treat two cases depending on the low pass graph filter's strength. When the graph filter is strong low pass, i.e., it has a frequency response that drops sharply at the high frequencies, we show that the principal component analysis (PCA) method detects central nodes with high accuracy. For general low pass graph filter, we show that the graph signals can be described by a structured factor model featuring the product between a low-rank plus sparse factor and an unstructured factor. We propose a two-stage decomposition algorithm to learn the structured factor model via a judicious combination of the non-negative matrix factorization and robust PCA algorithms. We analyze the identifiability conditions for the model which lead to accurate central nodes detection. Numerical experiments on synthetic and real data are provided to support our findings. We demonstrate significant performance gains over prior works.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge