Identifying First-order Lowpass Graph Signals using Perron Frobenius Theorem
Paper and Code
Jan 20, 2021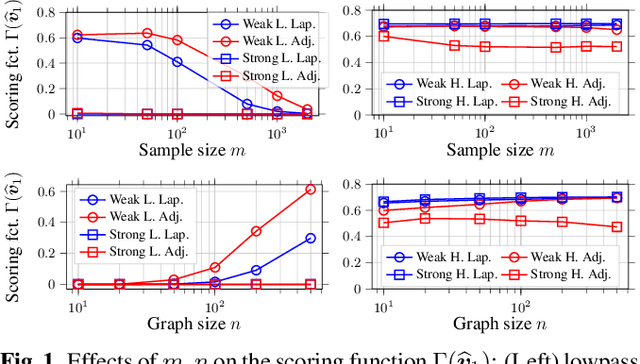
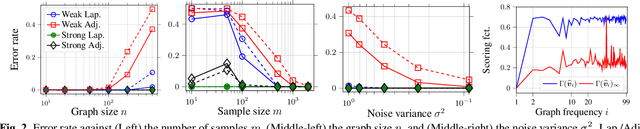
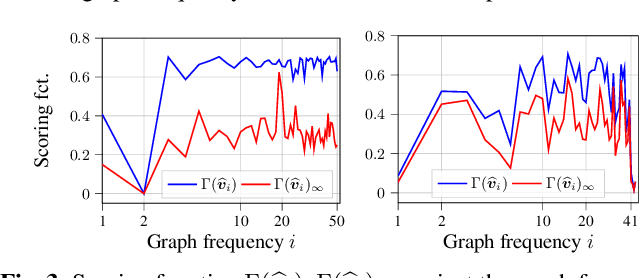
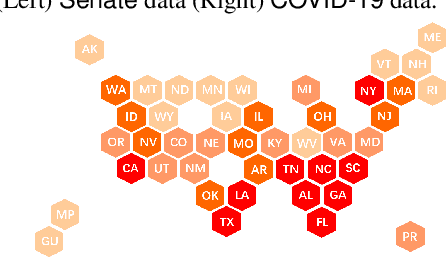
This paper is concerned with the blind identification of graph filters from graph signals. Our aim is to determine if the graph filter generating the graph signals is first-order lowpass without knowing the graph topology. Notice that lowpass graph filter is a common prerequisite for applying graph signal processing tools for sampling, denoising, and graph learning. Our method is inspired by the Perron Frobenius theorem, which observes that for first-order lowpass graph filter, the top eigenvector of output covariance would be the only eigenvector with elements of the same sign. Utilizing this observation, we develop a simple detector that answers if a given data set is produced by a first-order lowpass graph filter. We analyze the effects of finite-sample, graph size, observation noise, strength of lowpass filter, on the detector's performance. Numerical experiments on synthetic and real data support our findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge