HILL: Hierarchy-aware Information Lossless Contrastive Learning for Hierarchical Text Classification

Existing self-supervised methods in natural language processing (NLP), especially hierarchical text classification (HTC), mainly focus on self-supervised contrastive learning, extremely relying on human-designed augmentation rules to generate contrastive samples, which can potentially corrupt or distort the original information. In this paper, we tend to investigate the feasibility of a contrastive learning scheme in which the semantic and syntactic information inherent in the input sample is adequately reserved in the contrastive samples and fused during the learning process. Specifically, we propose an information lossless contrastive learning strategy for HTC, namely \textbf{H}ierarchy-aware \textbf{I}nformation \textbf{L}ossless contrastive \textbf{L}earning (HILL), which consists of a text encoder representing the input document, and a structure encoder directly generating the positive sample. The structure encoder takes the document embedding as input, extracts the essential syntactic information inherent in the label hierarchy with the principle of structural entropy minimization, and injects the syntactic information into the text representation via hierarchical representation learning. Experiments on three common datasets are conducted to verify the superiority of HILL.

A Simple yet Effective Method for Graph Classification

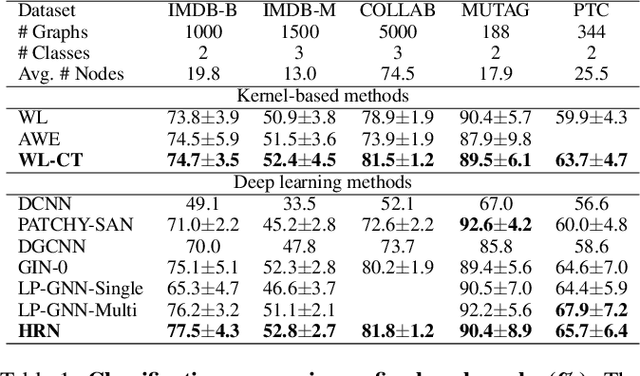
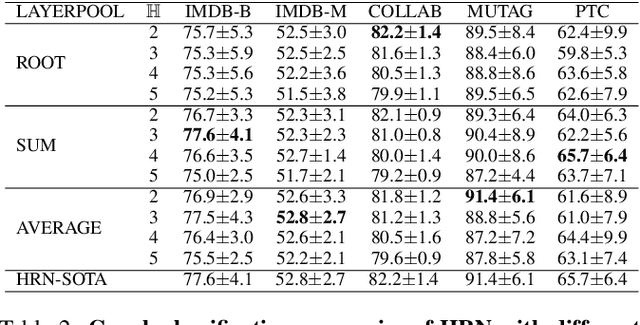
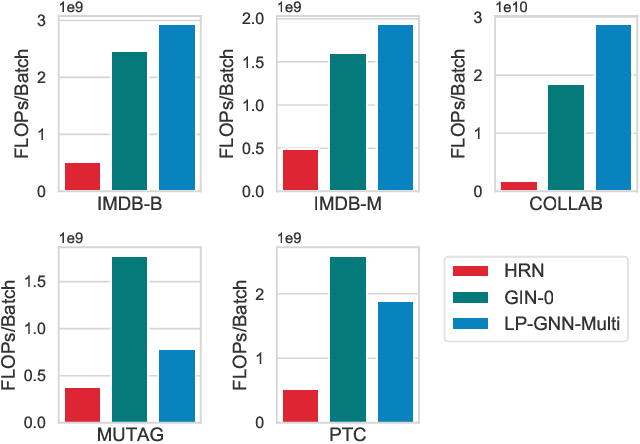
In deep neural networks, better results can often be obtained by increasing the complexity of previously developed basic models. However, it is unclear whether there is a way to boost performance by decreasing the complexity of such models. Intuitively, given a problem, a simpler data structure comes with a simpler algorithm. Here, we investigate the feasibility of improving graph classification performance while simplifying the learning process. Inspired by structural entropy on graphs, we transform the data sample from graphs to coding trees, which is a simpler but essential structure for graph data. Furthermore, we propose a novel message passing scheme, termed hierarchical reporting, in which features are transferred from leaf nodes to root nodes by following the hierarchical structure of coding trees. We then present a tree kernel and a convolutional network to implement our scheme for graph classification. With the designed message passing scheme, the tree kernel and convolutional network have a lower runtime complexity of $O(n)$ than Weisfeiler-Lehman subtree kernel and other graph neural networks of at least $O(hm)$. We empirically validate our methods with several graph classification benchmarks and demonstrate that they achieve better performance and lower computational consumption than competing approaches.

Structural Optimization Makes Graph Classification Simpler and Better

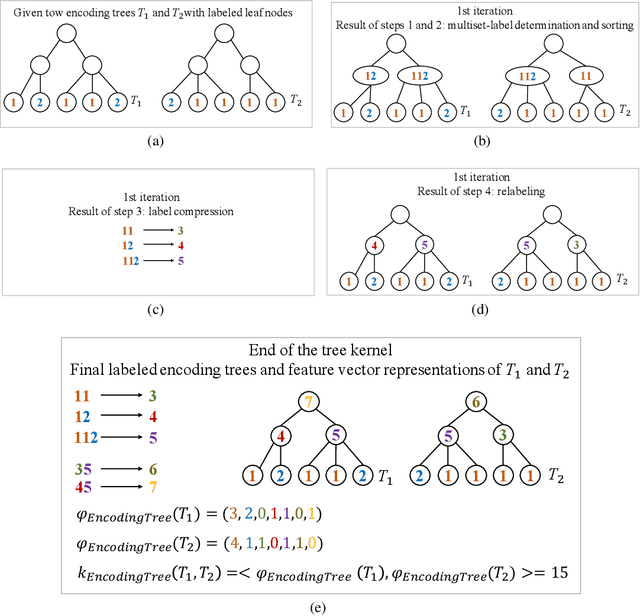
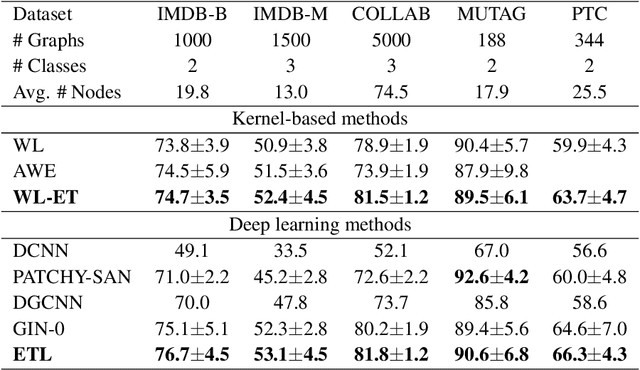
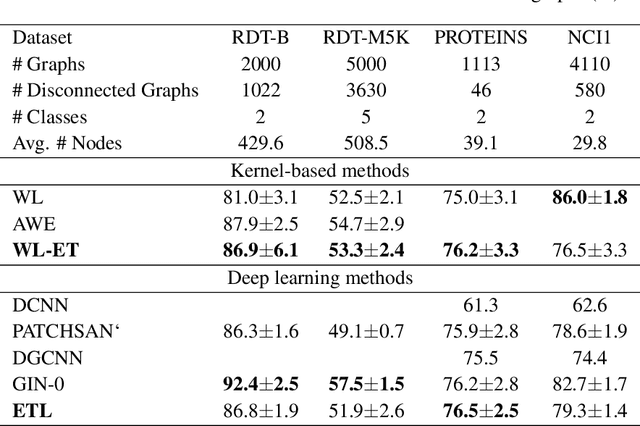
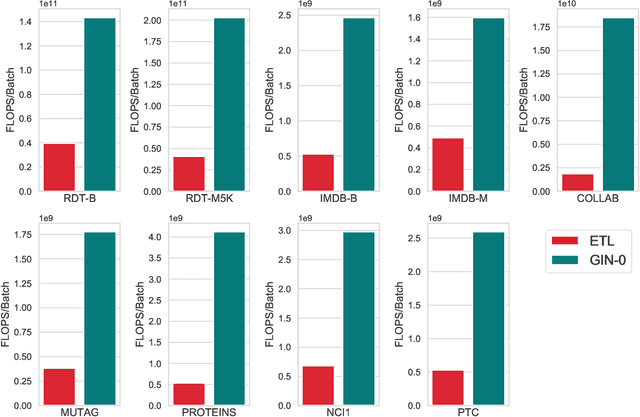
In deep neural networks, better results can often be obtained by increasing the complexity of previously developed basic models. However, it is unclear whether there is a way to boost performance by decreasing the complexity of such models. Here, based on an optimization method, we investigate the feasibility of improving graph classification performance while simplifying the model learning process. Inspired by progress in structural information assessment, we optimize the given data sample from graphs to encoding trees. In particular, we minimize the structural entropy of the transformed encoding tree to decode the key structure underlying a graph. This transformation is denoted as structural optimization. Furthermore, we propose a novel feature combination scheme, termed hierarchical reporting, for encoding trees. In this scheme, features are transferred from leaf nodes to root nodes by following the hierarchical structures of encoding trees. We then present an implementation of the scheme in a tree kernel and a convolutional network to perform graph classification. The tree kernel follows label propagation in the Weisfeiler-Lehman (WL) subtree kernel, but it has a lower runtime complexity $O(n)$. The convolutional network is a special implementation of our tree kernel in the deep learning field and is called Encoding Tree Learning (ETL). We empirically validate our tree kernel and convolutional network with several graph classification benchmarks and demonstrate that our methods achieve better performance and lower computational consumption than competing approaches.

An Information-theoretic Perspective of Hierarchical Clustering

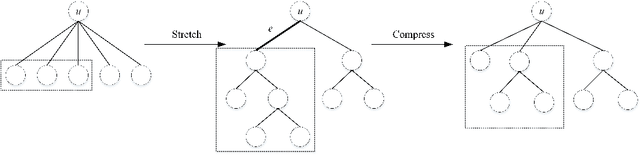
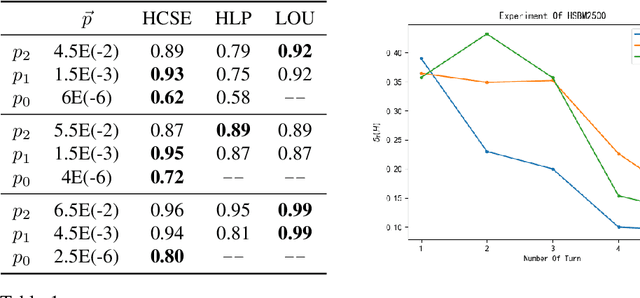
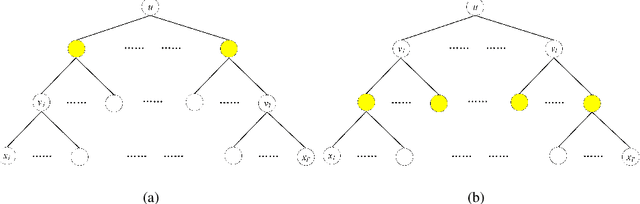
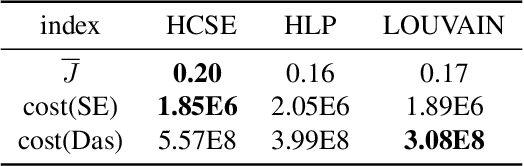
A combinatorial cost function for hierarchical clustering was introduced by Dasgupta \cite{dasgupta2016cost}. It has been generalized by Cohen-Addad et al. \cite{cohen2019hierarchical} to a general form named admissible function. In this paper, we investigate hierarchical clustering from the \emph{information-theoretic} perspective and formulate a new objective function. We also establish the relationship between these two perspectives. In algorithmic aspect, we get rid of the traditional top-down and bottom-up frameworks, and propose a new one to stratify the \emph{sparsest} level of a cluster tree recursively in guide with our objective function. For practical use, our resulting cluster tree is not binary. Our algorithm called HCSE outputs a $k$-level cluster tree by a novel and interpretable mechanism to choose $k$ automatically without any hyper-parameter. Our experimental results on synthetic datasets show that HCSE has a great advantage in finding the intrinsic number of hierarchies, and the results on real datasets show that HCSE also achieves competitive costs over the popular algorithms LOUVAIN and HLP.