Bingchen Fan
An Information-theoretic Perspective of Hierarchical Clustering
Aug 13, 2021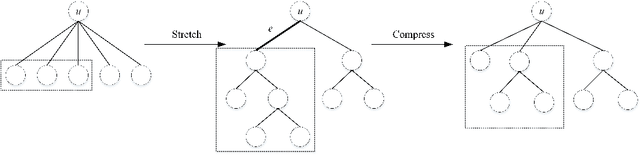
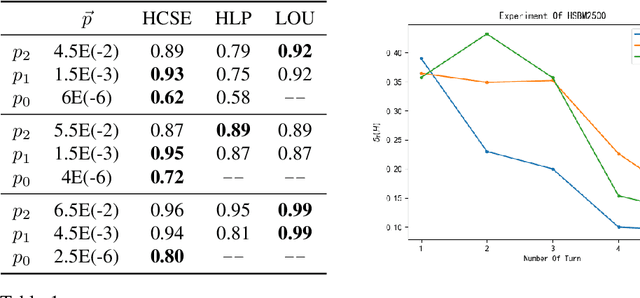
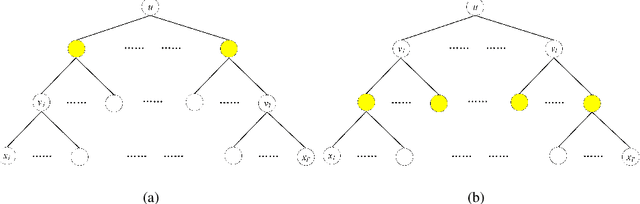
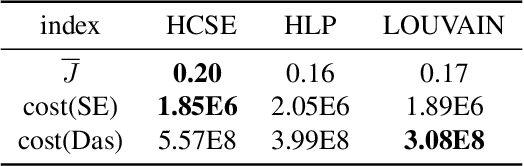
Abstract:A combinatorial cost function for hierarchical clustering was introduced by Dasgupta \cite{dasgupta2016cost}. It has been generalized by Cohen-Addad et al. \cite{cohen2019hierarchical} to a general form named admissible function. In this paper, we investigate hierarchical clustering from the \emph{information-theoretic} perspective and formulate a new objective function. We also establish the relationship between these two perspectives. In algorithmic aspect, we get rid of the traditional top-down and bottom-up frameworks, and propose a new one to stratify the \emph{sparsest} level of a cluster tree recursively in guide with our objective function. For practical use, our resulting cluster tree is not binary. Our algorithm called HCSE outputs a $k$-level cluster tree by a novel and interpretable mechanism to choose $k$ automatically without any hyper-parameter. Our experimental results on synthetic datasets show that HCSE has a great advantage in finding the intrinsic number of hierarchies, and the results on real datasets show that HCSE also achieves competitive costs over the popular algorithms LOUVAIN and HLP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge