Planning on a Budget: Safe Non-Conservative Planning in Probabilistic Dynamic Environments

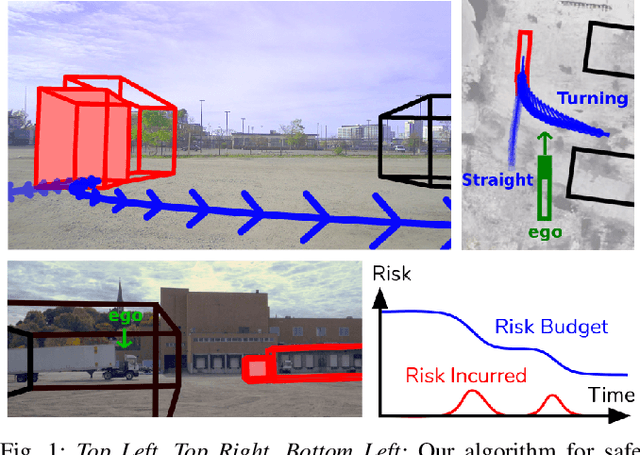
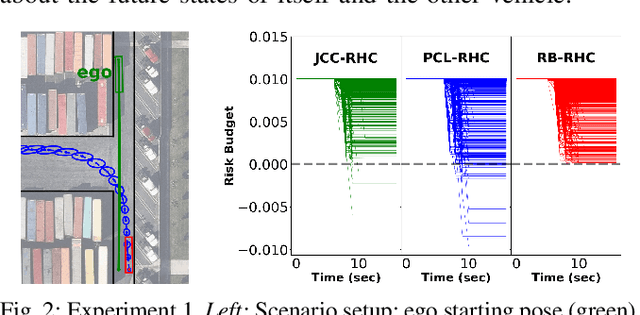
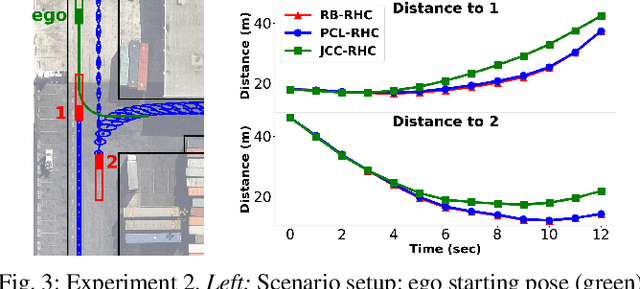
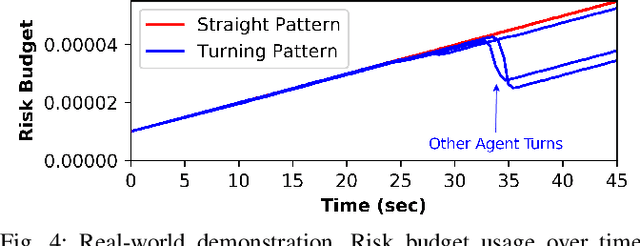
Planning in environments with other agents whose future actions are uncertain often requires compromise between safety and performance. Here our goal is to design efficient planning algorithms with guaranteed bounds on the probability of safety violation, which nonetheless achieve non-conservative performance. To quantify a system's risk, we define a natural criterion called interval risk bounds (IRBs), which provide a parametric upper bound on the probability of safety violation over a given time interval or task. We present a novel receding horizon algorithm, and prove that it can satisfy a desired IRB. Our algorithm maintains a dynamic risk budget which constrains the allowable risk at each iteration, and guarantees recursive feasibility by requiring a safe set to be reachable by a contingency plan within the budget. We empirically demonstrate that our algorithm is both safer and less conservative than strong baselines in two simulated autonomous driving experiments in scenarios involving collision avoidance with other vehicles, and additionally demonstrate our algorithm running on an autonomous class 8 truck.

PODDP: Partially Observable Differential Dynamic Programming for Latent Belief Space Planning

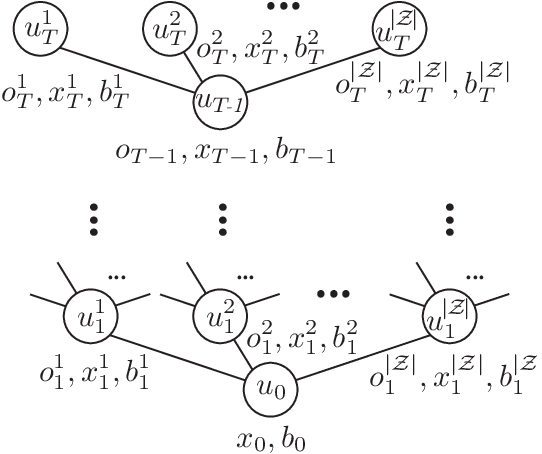
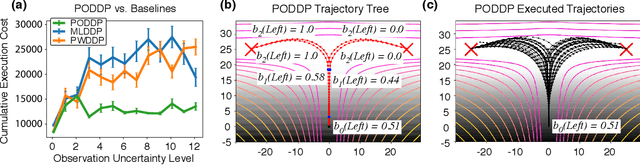
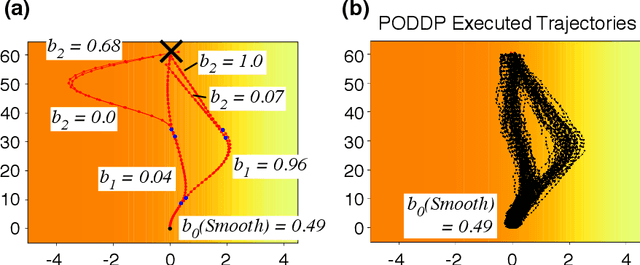
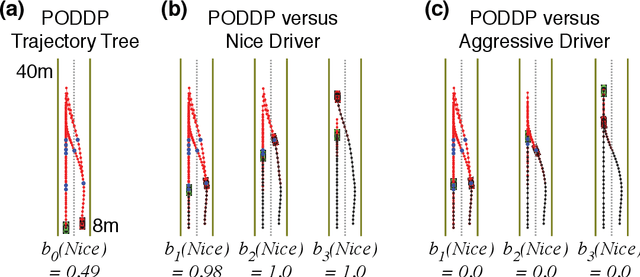
Autonomous agents are limited in their ability to observe the world state. Partially observable Markov decision processes (POMDPs) formally model the problem of planning under world state uncertainty, but POMDPs with continuous actions and nonlinear dynamics suitable for robotics applications are challenging to solve. In this paper, we present an efficient differential dynamic programming (DDP) algorithm for belief space planning in POMDPs with uncertainty over a discrete latent state, and continuous states, actions, observations, and nonlinear dynamics. This representation allows planning of dynamic trajectories which are sensitive to structured uncertainty over discrete latent world states. We develop dynamic programming techniques to optimize a contingency plan over a tree of possible observations and belief space trajectories, and also derive a hierarchical version of the algorithm. Our method is applicable to problems with uncertainty over the cost or reward function (e.g., the configuration of goals or obstacles), uncertainty over the dynamics (e.g., the dynamical mode of a hybrid system), and uncertainty about interactions, where other agents' behavior is conditioned on latent intentions. Benchmarks show that our algorithm outperforms popular heuristic approaches to planning under uncertainty, and results from an autonomous lane changing task demonstrate that our algorithm can synthesize robust interactive trajectories.

Learning Trajectory Prediction with Continuous Inverse Optimal Control via Langevin Sampling of Energy-Based Models

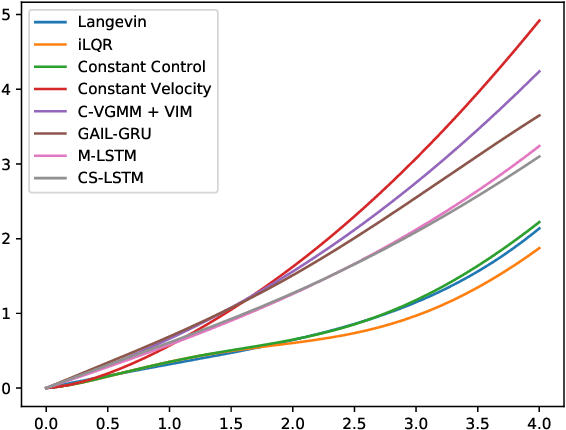
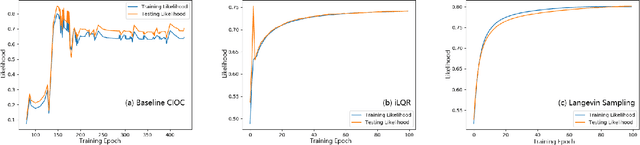
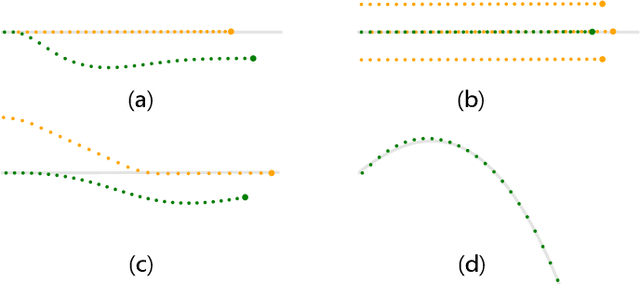
Autonomous driving is a challenging multiagent domain which requires optimizing complex, mixed cooperative-competitive interactions. Learning to predict contingent distributions over other vehicles' trajectories simplifies the problem, allowing approximate solutions by trajectory optimization with dynamic constraints. We take a model-based approach to prediction, in order to make use of structured prior knowledge of vehicle kinematics, and the assumption that other drivers plan trajectories to minimize an unknown cost function. We introduce a novel inverse optimal control (IOC) algorithm to learn other vehicles' cost functions in an energy-based generative model. Langevin Sampling, a Monte Carlo based sampling algorithm, is used to directly sample the control sequence. Our algorithm provides greater flexibility than standard IOC methods, and can learn higher-level, non-Markovian cost functions defined over entire trajectories. We extend weighted feature-based cost functions with neural networks to obtain NN-augmented cost functions, which combine the advantages of both model-based and model-free learning. Results show that model-based IOC can achieve state-of-the-art vehicle trajectory prediction accuracy, and naturally take scene information into account.

Multi-Agent Tensor Fusion for Contextual Trajectory Prediction

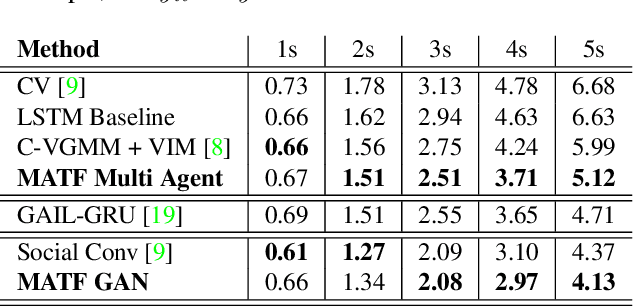
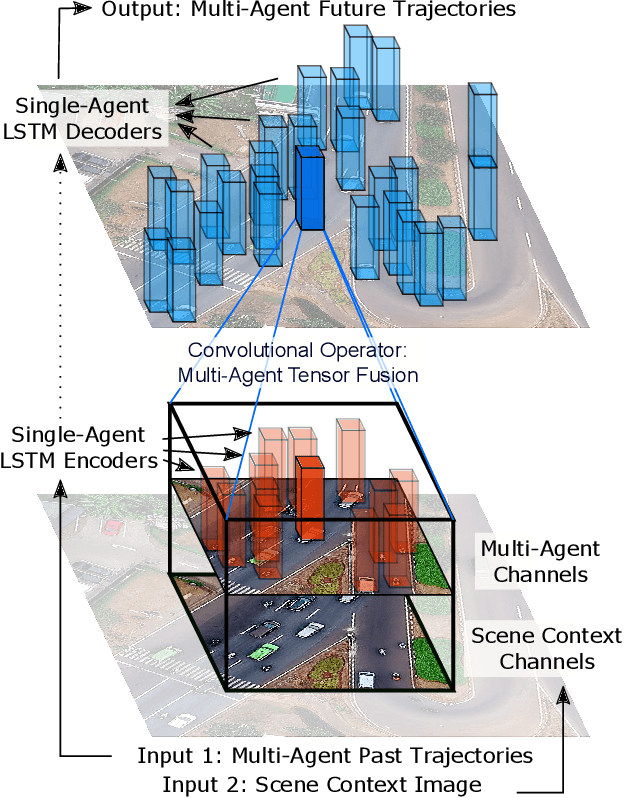
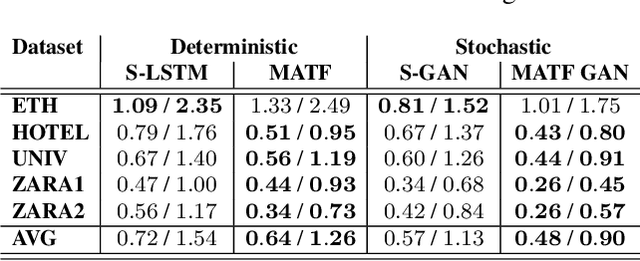
Accurate prediction of others' trajectories is essential for autonomous driving. Trajectory prediction is challenging because it requires reasoning about agents' past movements, social interactions among varying numbers and kinds of agents, constraints from the scene context, and the stochasticity of human behavior. Our approach models these interactions and constraints jointly within a novel Multi-Agent Tensor Fusion (MATF) network. Specifically, the model encodes multiple agents' past trajectories and the scene context into a Multi-Agent Tensor, then applies convolutional fusion to capture multiagent interactions while retaining the spatial structure of agents and the scene context. The model decodes recurrently to multiple agents' future trajectories, using adversarial loss to learn stochastic predictions. Experiments on both highway driving and pedestrian crowd datasets show that the model achieves state-of-the-art prediction accuracy.