Optimised Storage for Datalog Reasoning

Materialisation facilitates Datalog reasoning by precomputing all consequences of the facts and the rules so that queries can be directly answered over the materialised facts. However, storing all materialised facts may be infeasible in practice, especially when the rules are complex and the given set of facts is large. We observe that for certain combinations of rules, there exist data structures that compactly represent the reasoning result and can be efficiently queried when necessary. In this paper, we present a general framework that allows for the integration of such optimised storage schemes with standard materialisation algorithms. Moreover, we devise optimised storage schemes targeting at transitive rules and union rules, two types of (combination of) rules that commonly occur in practice. Our experimental evaluation shows that our approach significantly improves memory consumption, sometimes by orders of magnitude, while remaining competitive in terms of query answering time.

Enhancing Datalog Reasoning with Hypertree Decompositions

Datalog reasoning based on the semina\"ive evaluation strategy evaluates rules using traditional join plans, which often leads to redundancy and inefficiency in practice, especially when the rules are complex. Hypertree decompositions help identify efficient query plans and reduce similar redundancy in query answering. However, it is unclear how this can be applied to materialisation and incremental reasoning with recursive Datalog programs. Moreover, hypertree decompositions require additional data structures and thus introduce nonnegligible overhead in both runtime and memory consumption. In this paper, we provide algorithms that exploit hypertree decompositions for the materialisation and incremental evaluation of Datalog programs. Furthermore, we combine this approach with standard Datalog reasoning algorithms in a modular fashion so that the overhead caused by the decompositions is reduced. Our empirical evaluation shows that, when the program contains complex rules, the combined approach is usually significantly faster than the baseline approach, sometimes by orders of magnitude.

Data Science with Vadalog: Bridging Machine Learning and Reasoning

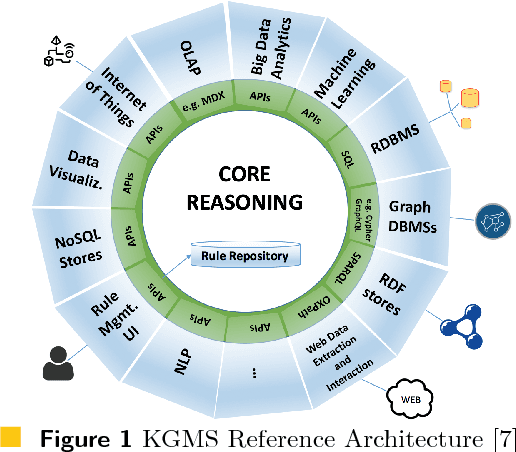
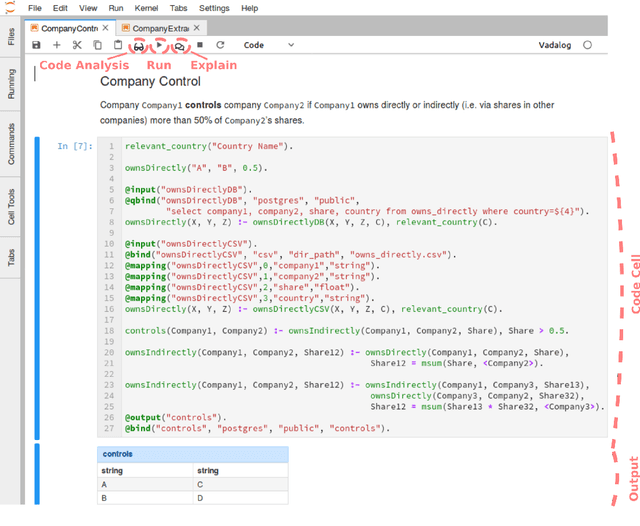
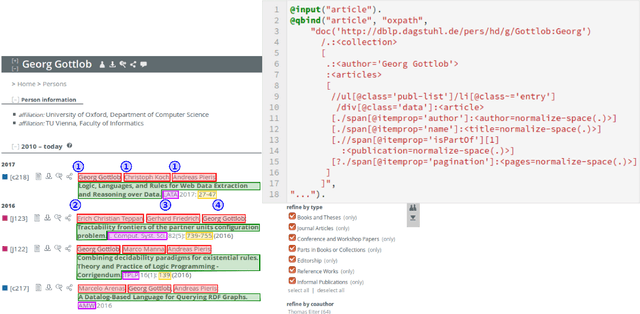
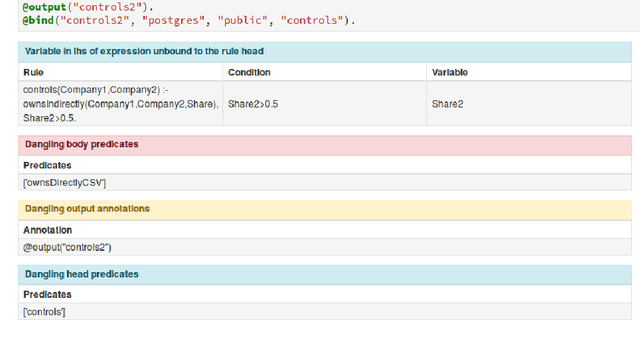
Following the recent successful examples of large technology companies, many modern enterprises seek to build knowledge graphs to provide a unified view of corporate knowledge and to draw deep insights using machine learning and logical reasoning. There is currently a perceived disconnect between the traditional approaches for data science, typically based on machine learning and statistical modelling, and systems for reasoning with domain knowledge. In this paper we present a state-of-the-art Knowledge Graph Management System, Vadalog, which delivers highly expressive and efficient logical reasoning and provides seamless integration with modern data science toolkits, such as the Jupyter platform. We demonstrate how to use Vadalog to perform traditional data wrangling tasks, as well as complex logical and probabilistic reasoning. We argue that this is a significant step forward towards combining machine learning and reasoning in data science.

Handling owl:sameAs via Rewriting

Rewriting is widely used to optimise owl:sameAs reasoning in materialisation based OWL 2 RL systems. We investigate issues related to both the correctness and efficiency of rewriting, and present an algorithm that guarantees correctness, improves efficiency, and can be effectively parallelised. Our evaluation shows that our approach can reduce reasoning times on practical data sets by orders of magnitude.

Datalog Rewritability of Disjunctive Datalog Programs and its Applications to Ontology Reasoning

We study the problem of rewriting a disjunctive datalog program into plain datalog. We show that a disjunctive program is rewritable if and only if it is equivalent to a linear disjunctive program, thus providing a novel characterisation of datalog rewritability. Motivated by this result, we propose weakly linear disjunctive datalog---a novel rule-based KR language that extends both datalog and linear disjunctive datalog and for which reasoning is tractable in data complexity. We then explore applications of weakly linear programs to ontology reasoning and propose a tractable extension of OWL 2 RL with disjunctive axioms. Our empirical results suggest that many non-Horn ontologies can be reduced to weakly linear programs and that query answering over such ontologies using a datalog engine is feasible in practice.