Lipschitz regularized gradient flows and latent generative particles

Lipschitz regularized f-divergences are constructed by imposing a bound on the Lipschitz constant of the discriminator in the variational representation. They interpolate between the Wasserstein metric and f-divergences and provide a flexible family of loss functions for non-absolutely continuous (e.g. empirical) distributions, possibly with heavy tails. We construct Lipschitz regularized gradient flows on the space of probability measures based on these divergences. Examples of such gradient flows are Lipschitz regularized Fokker-Planck and porous medium partial differential equations (PDEs) for the Kullback-Leibler and alpha-divergences, respectively. The regularization corresponds to imposing a Courant-Friedrichs-Lewy numerical stability condition on the PDEs. For empirical measures, the Lipschitz regularization on gradient flows induces a numerically stable transporter/discriminator particle algorithm, where the generative particles are transported along the gradient of the discriminator. The gradient structure leads to a regularized Fisher information (particle kinetic energy) used to track the convergence of the algorithm. The Lipschitz regularized discriminator can be implemented via neural network spectral normalization and the particle algorithm generates approximate samples from possibly high-dimensional distributions known only from data. Notably, our particle algorithm can generate synthetic data even in small sample size regimes. A new data processing inequality for the regularized divergence allows us to combine our particle algorithm with representation learning, e.g. autoencoder architectures. The resulting algorithm yields markedly improved generative properties in terms of efficiency and quality of the synthetic samples. From a statistical mechanics perspective the encoding can be interpreted dynamically as learning a better mobility for the generative particles.

Function-space regularized Rényi divergences

We propose a new family of regularized R\'enyi divergences parametrized not only by the order $\alpha$ but also by a variational function space. These new objects are defined by taking the infimal convolution of the standard R\'enyi divergence with the integral probability metric (IPM) associated with the chosen function space. We derive a novel dual variational representation that can be used to construct numerically tractable divergence estimators. This representation avoids risk-sensitive terms and therefore exhibits lower variance, making it well-behaved when $\alpha>1$; this addresses a notable weakness of prior approaches. We prove several properties of these new divergences, showing that they interpolate between the classical R\'enyi divergences and IPMs. We also study the $\alpha\to\infty$ limit, which leads to a regularized worst-case-regret and a new variational representation in the classical case. Moreover, we show that the proposed regularized R\'enyi divergences inherit features from IPMs such as the ability to compare distributions that are not absolutely continuous, e.g., empirical measures and distributions with low-dimensional support. We present numerical results on both synthetic and real datasets, showing the utility of these new divergences in both estimation and GAN training applications; in particular, we demonstrate significantly reduced variance and improved training performance.

Forward Looking Best-Response Multiplicative Weights Update Methods

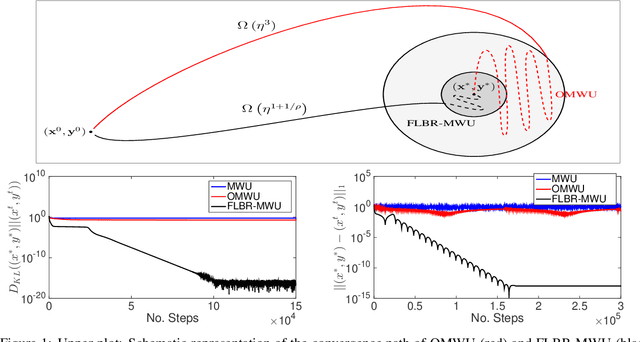
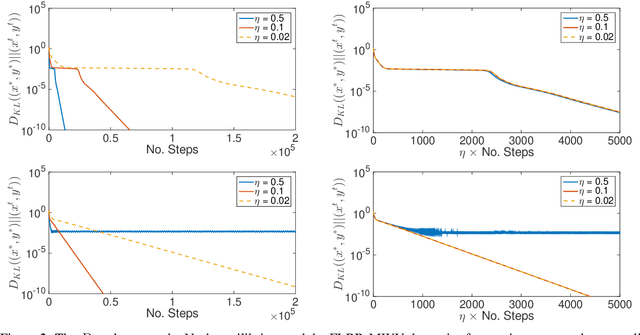
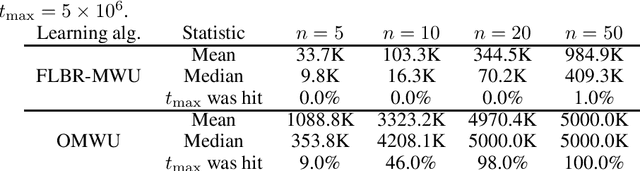
We propose a novel variant of the \emph{multiplicative weights update method} with forward-looking best-response strategies, that guarantees last-iterate convergence for \emph{zero-sum games} with a unique \emph{Nash equilibrium}. Particularly, we show that the proposed algorithm converges to an $\eta^{1/\rho}$-approximate Nash equilibrium, with $\rho > 1$, by decreasing the Kullback-Leibler divergence of each iterate by a rate of at least $\Omega(\eta^{1+\frac{1}{\rho}})$, for sufficiently small learning rate $\eta$. When our method enters a sufficiently small neighborhood of the solution, it becomes a contraction and converges to the Nash equilibrium of the game. Furthermore, we perform an experimental comparison with the recently proposed optimistic variant of the multiplicative weights update method, by \cite{Daskalakis2019LastIterateCZ}, which has also been proved to attain last-iterate convergence. Our findings reveal that our algorithm offers substantial gains both in terms of the convergence rate and the region of contraction relative to the previous approach.

Inference of Stochastic Dynamical Systems from Cross-Sectional Population Data

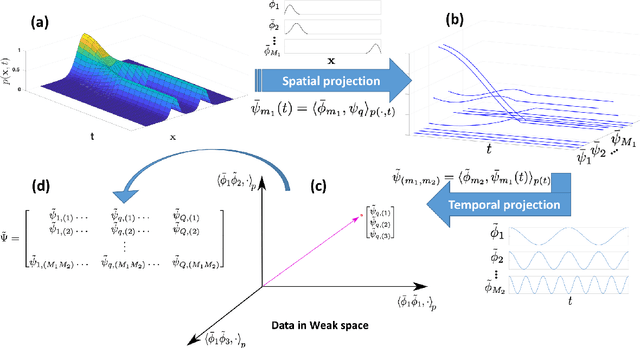
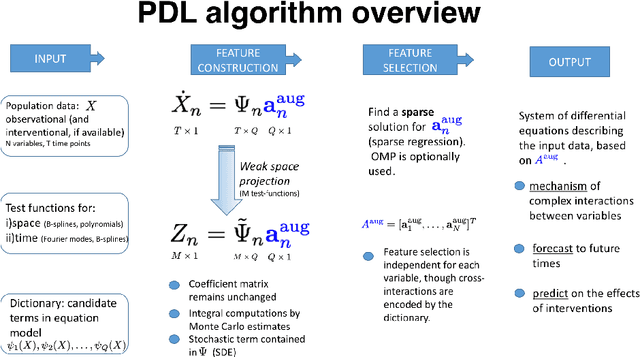
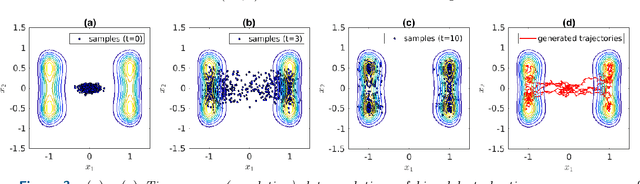
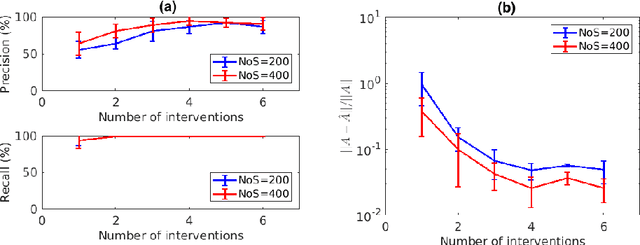
Inferring the driving equations of a dynamical system from population or time-course data is important in several scientific fields such as biochemistry, epidemiology, financial mathematics and many others. Despite the existence of algorithms that learn the dynamics from trajectorial measurements there are few attempts to infer the dynamical system straight from population data. In this work, we deduce and then computationally estimate the Fokker-Planck equation which describes the evolution of the population's probability density, based on stochastic differential equations. Then, following the USDL approach, we project the Fokker-Planck equation to a proper set of test functions, transforming it into a linear system of equations. Finally, we apply sparse inference methods to solve the latter system and thus induce the driving forces of the dynamical system. Our approach is illustrated in both synthetic and real data including non-linear, multimodal stochastic differential equations, biochemical reaction networks as well as mass cytometry biological measurements.

$(f,Γ)$-Divergences: Interpolating between $f$-Divergences and Integral Probability Metrics

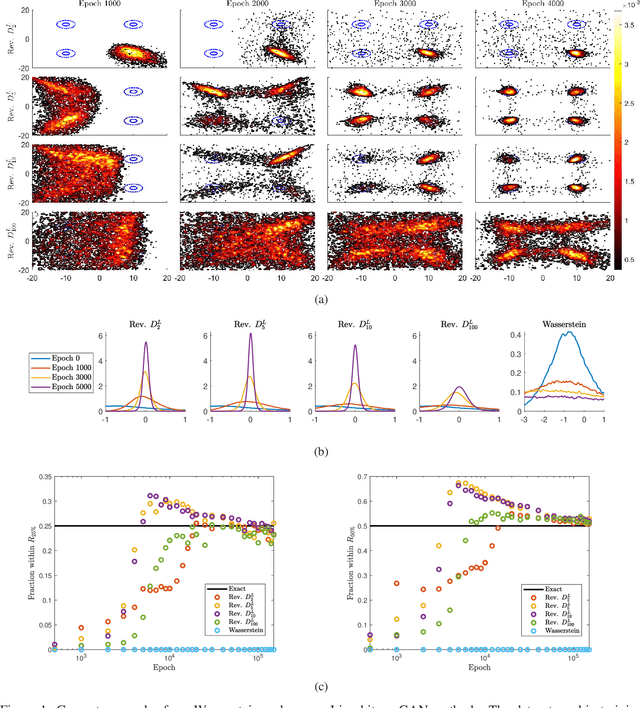
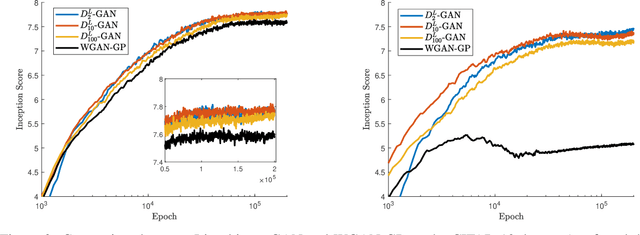
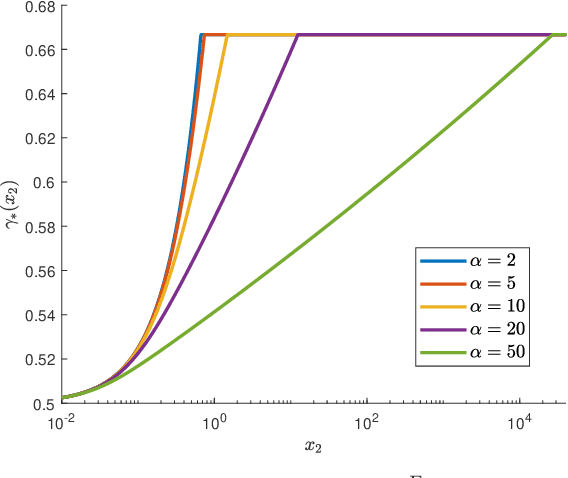
We develop a general framework for constructing new information-theoretic divergences that rigorously interpolate between $f$-divergences and integral probability metrics (IPMs), such as the Wasserstein distance. These new divergences inherit features from IPMs, such as the ability to compare distributions which are not absolute continuous, as well as from $f$-divergences, for instance the strict concavity of their variational representations and the ability to compare heavy-tailed distributions. When combined, these features establish a divergence with improved convergence and estimation properties for statistical learning applications. We demonstrate their use in the training of generative adversarial networks (GAN) for heavy-tailed data and also show they can provide improved performance over gradient-penalized Wasserstein GAN in image generation.

Enhancing Speech Intelligibility in Text-To-Speech Synthesis using Speaking Style Conversion

The increased adoption of digital assistants makes text-to-speech (TTS) synthesis systems an indispensable feature of modern mobile devices. It is hence desirable to build a system capable of generating highly intelligible speech in the presence of noise. Past studies have investigated style conversion in TTS synthesis, yet degraded synthesized quality often leads to worse intelligibility. To overcome such limitations, we proposed a novel transfer learning approach using Tacotron and WaveRNN based TTS synthesis. The proposed speech system exploits two modification strategies: (a) Lombard speaking style data and (b) Spectral Shaping and Dynamic Range Compression (SSDRC) which has been shown to provide high intelligibility gains by redistributing the signal energy on the time-frequency domain. We refer to this extension as Lombard-SSDRC TTS system. Intelligibility enhancement as quantified by the Intelligibility in Bits (SIIB-Gauss) measure shows that the proposed Lombard-SSDRC TTS system shows significant relative improvement between 110% and 130% in speech-shaped noise (SSN), and 47% to 140% in competing-speaker noise (CSN) against the state-of-the-art TTS approach. Additional subjective evaluation shows that Lombard-SSDRC TTS successfully increases the speech intelligibility with relative improvement of 455% for SSN and 104% for CSN in median keyword correction rate compared to the baseline TTS method.

Speaker Conditional WaveRNN: Towards Universal Neural Vocoder for Unseen Speaker and Recording Conditions

Recent advancements in deep learning led to human-level performance in single-speaker speech synthesis. However, there are still limitations in terms of speech quality when generalizing those systems into multiple-speaker models especially for unseen speakers and unseen recording qualities. For instance, conventional neural vocoders are adjusted to the training speaker and have poor generalization capabilities to unseen speakers. In this work, we propose a variant of WaveRNN, referred to as speaker conditional WaveRNN (SC-WaveRNN). We target towards the development of an efficient universal vocoder even for unseen speakers and recording conditions. In contrast to standard WaveRNN, SC-WaveRNN exploits additional information given in the form of speaker embeddings. Using publicly-available data for training, SC-WaveRNN achieves significantly better performance over baseline WaveRNN on both subjective and objective metrics. In MOS, SC-WaveRNN achieves an improvement of about 23% for seen speaker and seen recording condition and up to 95% for unseen speaker and unseen condition. Finally, we extend our work by implementing a multi-speaker text-to-speech (TTS) synthesis similar to zero-shot speaker adaptation. In terms of performance, our system has been preferred over the baseline TTS system by 60% over 15.5% and by 60.9% over 32.6%, for seen and unseen speakers, respectively.

Optimizing variational representations of divergences and accelerating their statistical estimation

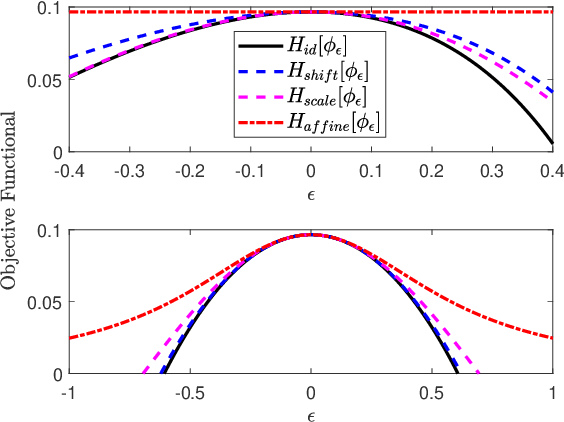
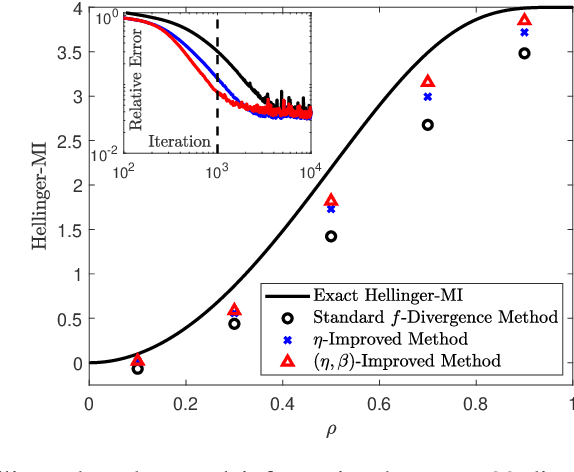
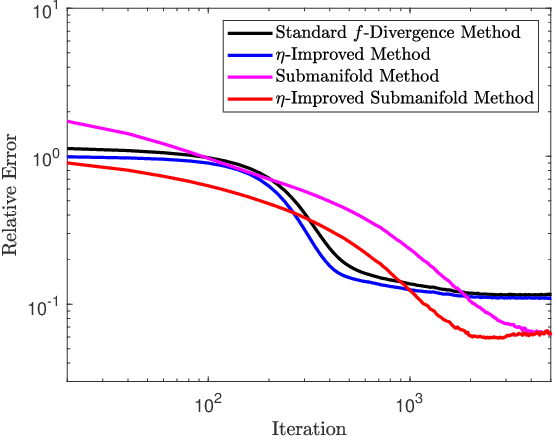
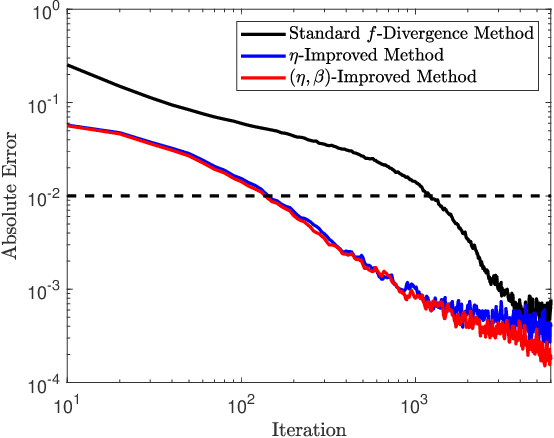
Variational representations of distances and divergences between high-dimensional probability distributions offer significant theoretical insights and practical advantages in numerous research areas. Recently, they have gained popularity in machine learning as a tractable and scalable approach for training probabilistic models and statistically differentiate between data distributions. Their advantages include: 1) They can be estimated from data. 2) Such representations can leverage the ability of neural networks to efficiently approximate optimal solutions in function spaces. However, a systematic and practical approach to improving the tightness of such variational formulas, and accordingly accelerate statistical learning and estimation from data, is currently lacking. Here we develop a systematic methodology for building new, tighter variational representations of divergences. Our approach relies on improved objective functionals constructed via an auxiliary optimization problem. Furthermore, the calculation of the functional Hessian of objective functionals unveils the local curvature differences around the common optimal variational solution; this allows us to quantify and order relative tightness gains between different variational representations. Finally, numerical simulations utilizing neural network optimization demonstrate that tighter representations can result in significantly faster learning and more accurate estimation of divergences in both synthetic and real datasets (of more than 700 dimensions), often accelerated by nearly an order of magnitude.

Predictive modeling approaches in laser-based material processing

Predictive modelling represents an emerging field that combines existing and novel methodologies aimed to rapidly understand physical mechanisms and concurrently develop new materials, processes and structures. In the current study, previously-unexplored predictive modelling in a key-enabled technology, the laser-based manufacturing, aims to automate and forecast the effect of laser processing on material structures. The focus is centred on the performance of representative statistical and machine learning algorithms in predicting the outcome of laser processing on a range of materials. Results on experimental data showed that predictive models were able to satisfactorily learn the mapping between the laser input variables and the observed material structure. These results are further integrated with simulation data aiming to elucidate the multiscale physical processes upon laser-material interaction. As a consequence, we augmented the adjusted simulated data to the experimental and substantially improved the predictive performance, due to the availability of increased number of sampling points. In parallel, a metric to identify and quantify the regions with high predictive uncertainty, is presented, revealing that high uncertainty occurs around the transition boundaries. Our results can set the basis for a systematic methodology towards reducing material design, testing and production cost via the replacement of expensive trial-and-error based manufacturing procedure with a precise pre-fabrication predictive tool.

Cumulant GAN

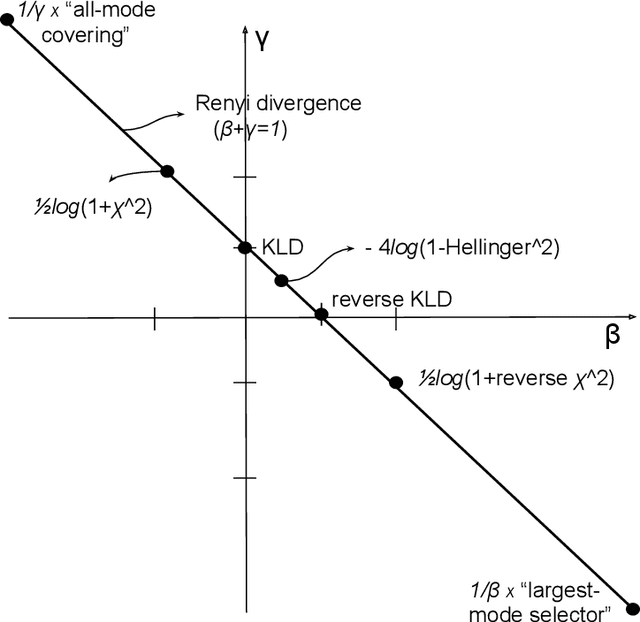
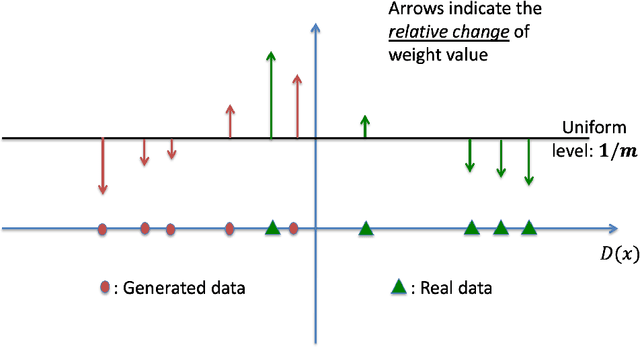
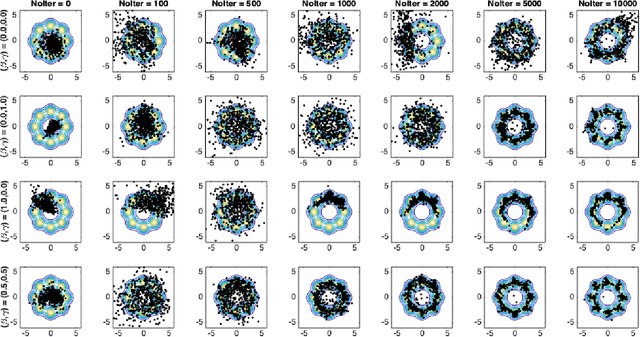
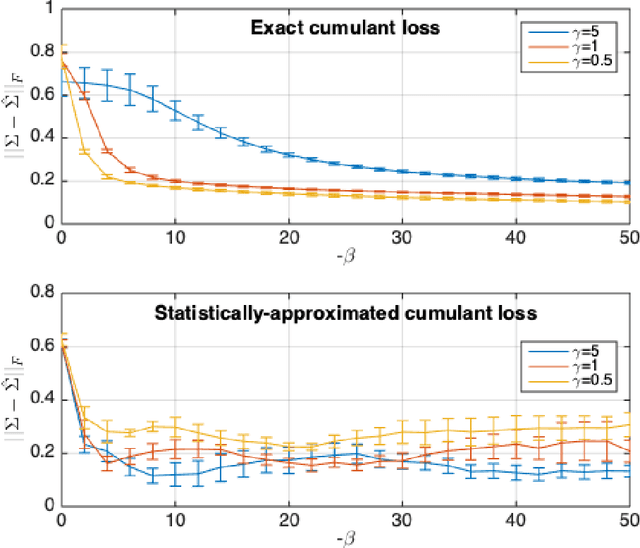
Despite the continuous improvements of Generative Adversarial Networks (GANs), stability and performance challenges still remain. In this work, we propose a novel loss function for GAN training aiming both for deeper theoretical understanding and improved performance of the underlying optimization problem. The new loss function is based on cumulant generating functions and relies on a recently-derived variational formula. We show that the corresponding optimization is equivalent to R\'enyi divergence minimization, thus offering a (partially) unified perspective of GAN losses: the R\'enyi family encompasses Kullback-Leibler divergence (KLD), reverse KLD, Hellinger distance and $\chi^2$-divergence. Wasserstein loss function is also included in the proposed cumulant GAN formulation. In terms of stability, we rigorously prove the convergence of the gradient descent algorithm for linear generator and linear discriminator for Gaussian distributions. Moreover, we numerically show that synthetic image generation trained on CIFAR-10 dataset is substantially improved in terms of inception score when weaker discriminators are considered.