Cumulant GAN
Paper and Code
Jun 11, 2020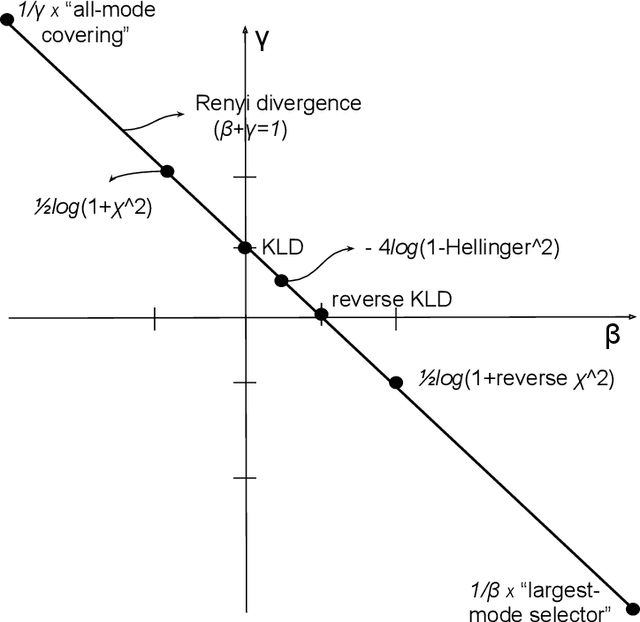
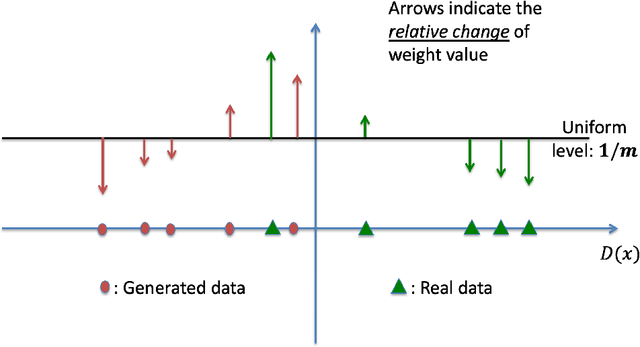
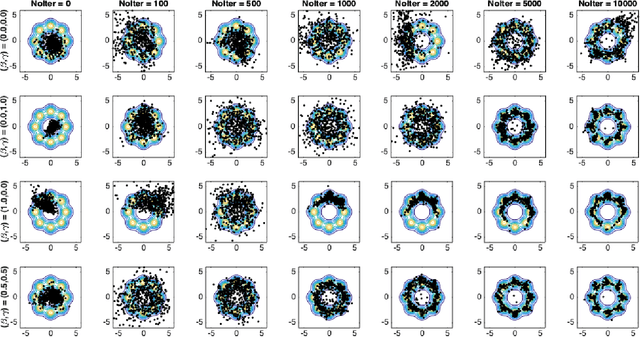
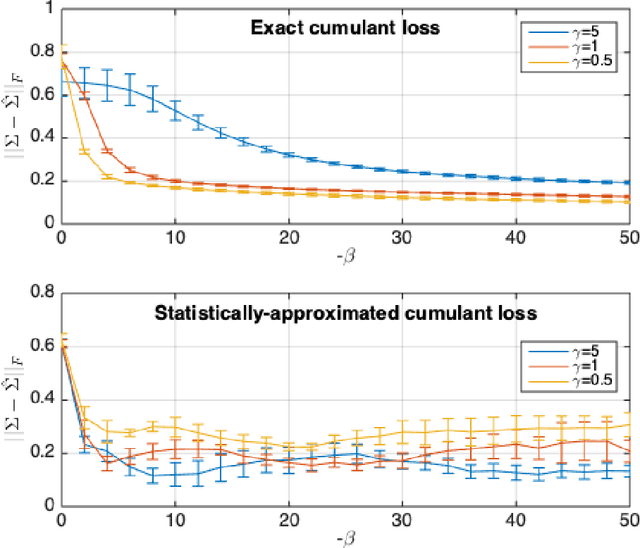
Despite the continuous improvements of Generative Adversarial Networks (GANs), stability and performance challenges still remain. In this work, we propose a novel loss function for GAN training aiming both for deeper theoretical understanding and improved performance of the underlying optimization problem. The new loss function is based on cumulant generating functions and relies on a recently-derived variational formula. We show that the corresponding optimization is equivalent to R\'enyi divergence minimization, thus offering a (partially) unified perspective of GAN losses: the R\'enyi family encompasses Kullback-Leibler divergence (KLD), reverse KLD, Hellinger distance and $\chi^2$-divergence. Wasserstein loss function is also included in the proposed cumulant GAN formulation. In terms of stability, we rigorously prove the convergence of the gradient descent algorithm for linear generator and linear discriminator for Gaussian distributions. Moreover, we numerically show that synthetic image generation trained on CIFAR-10 dataset is substantially improved in terms of inception score when weaker discriminators are considered.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge