Michail Fasoulakis
Forward Looking Best-Response Multiplicative Weights Update Methods
Jun 07, 2021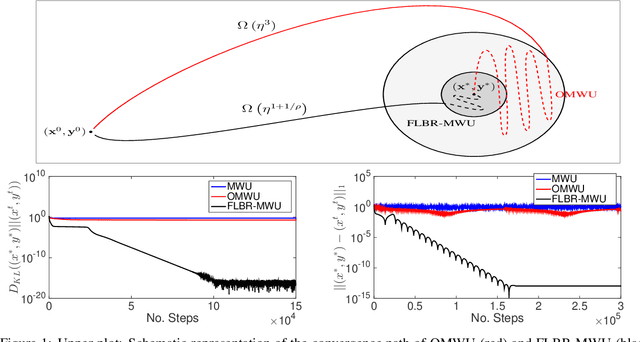

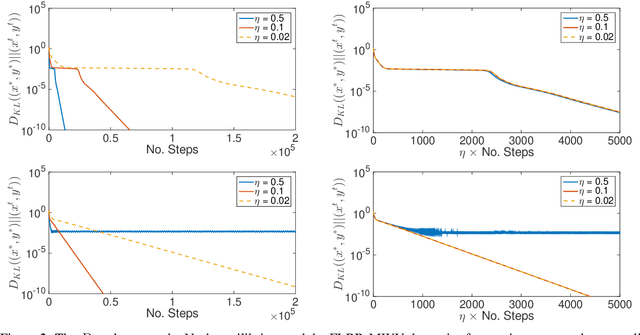
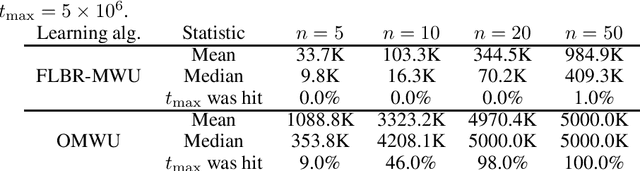
Abstract:We propose a novel variant of the \emph{multiplicative weights update method} with forward-looking best-response strategies, that guarantees last-iterate convergence for \emph{zero-sum games} with a unique \emph{Nash equilibrium}. Particularly, we show that the proposed algorithm converges to an $\eta^{1/\rho}$-approximate Nash equilibrium, with $\rho > 1$, by decreasing the Kullback-Leibler divergence of each iterate by a rate of at least $\Omega(\eta^{1+\frac{1}{\rho}})$, for sufficiently small learning rate $\eta$. When our method enters a sufficiently small neighborhood of the solution, it becomes a contraction and converges to the Nash equilibrium of the game. Furthermore, we perform an experimental comparison with the recently proposed optimistic variant of the multiplicative weights update method, by \cite{Daskalakis2019LastIterateCZ}, which has also been proved to attain last-iterate convergence. Our findings reveal that our algorithm offers substantial gains both in terms of the convergence rate and the region of contraction relative to the previous approach.
Cumulant GAN
Jun 11, 2020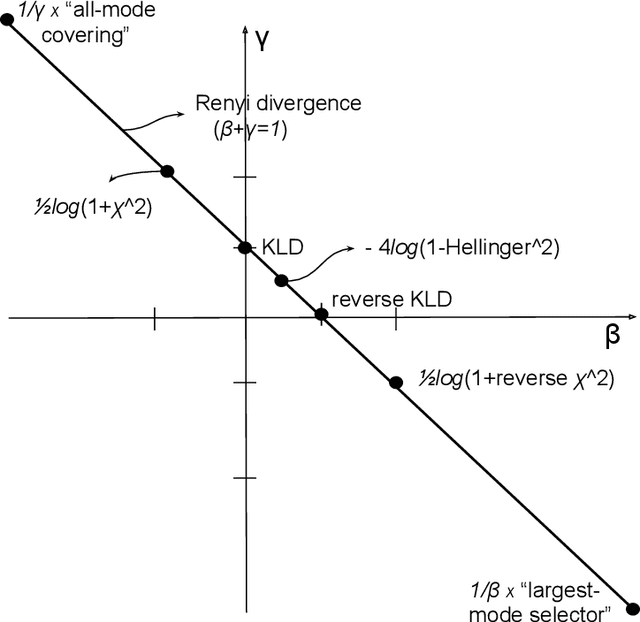
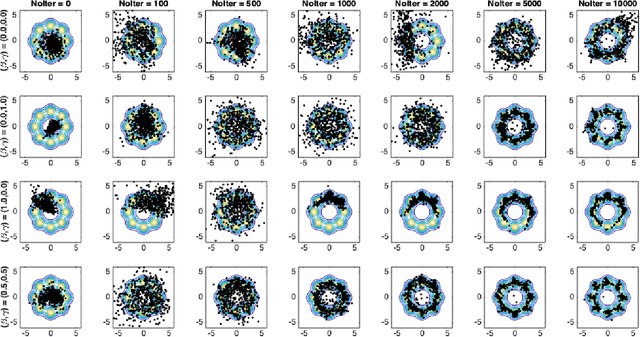
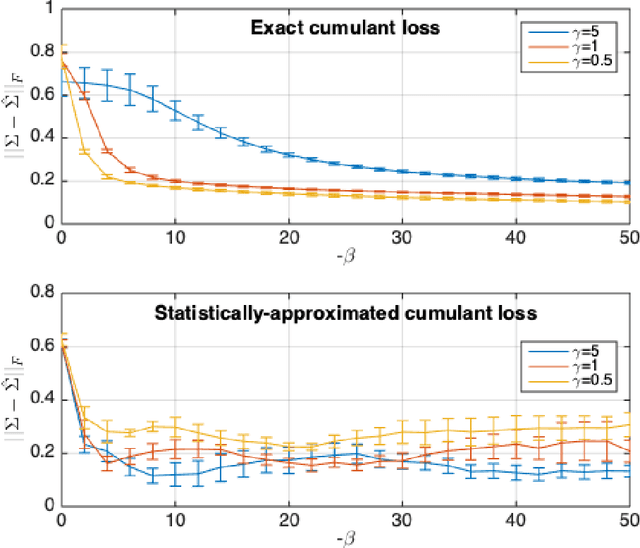
Abstract:Despite the continuous improvements of Generative Adversarial Networks (GANs), stability and performance challenges still remain. In this work, we propose a novel loss function for GAN training aiming both for deeper theoretical understanding and improved performance of the underlying optimization problem. The new loss function is based on cumulant generating functions and relies on a recently-derived variational formula. We show that the corresponding optimization is equivalent to R\'enyi divergence minimization, thus offering a (partially) unified perspective of GAN losses: the R\'enyi family encompasses Kullback-Leibler divergence (KLD), reverse KLD, Hellinger distance and $\chi^2$-divergence. Wasserstein loss function is also included in the proposed cumulant GAN formulation. In terms of stability, we rigorously prove the convergence of the gradient descent algorithm for linear generator and linear discriminator for Gaussian distributions. Moreover, we numerically show that synthetic image generation trained on CIFAR-10 dataset is substantially improved in terms of inception score when weaker discriminators are considered.
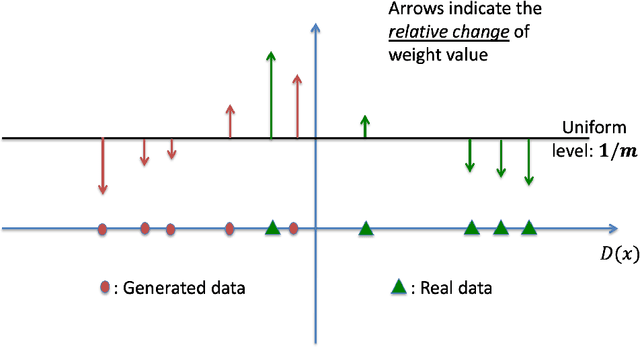
Training Generative Adversarial Networks with Weights
Nov 06, 2018
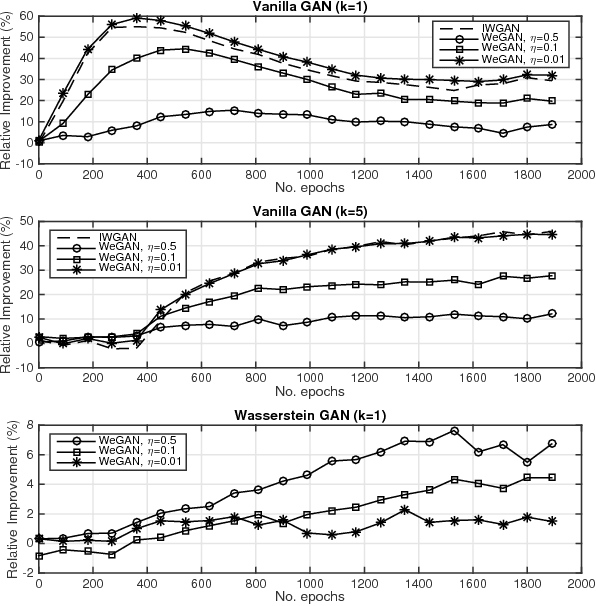
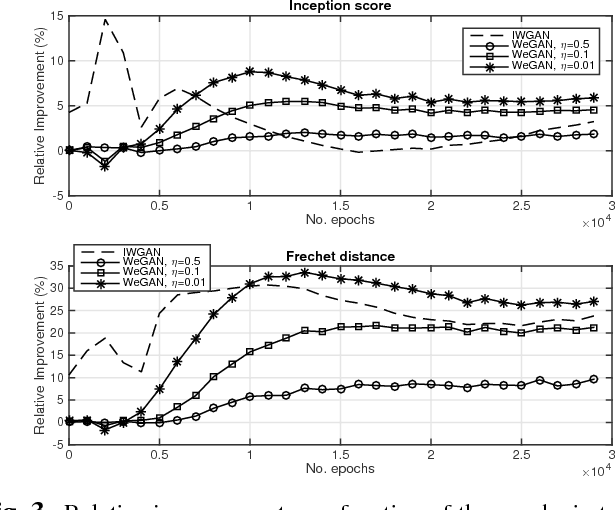
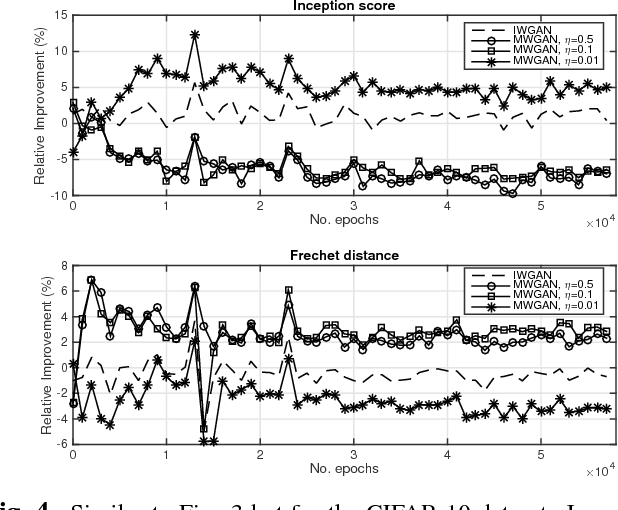
Abstract:The impressive success of Generative Adversarial Networks (GANs) is often overshadowed by the difficulties in their training. Despite the continuous efforts and improvements, there are still open issues regarding their convergence properties. In this paper, we propose a simple training variation where suitable weights are defined and assist the training of the Generator. We provide theoretical arguments why the proposed algorithm is better than the baseline training in the sense of speeding up the training process and of creating a stronger Generator. Performance results showed that the new algorithm is more accurate in both synthetic and image datasets resulting in improvements ranging between 5% and 50%.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge