TRIFFID: Autonomous Robotic Aid For Increasing First Responders Efficiency

The increasing complexity of natural disaster incidents demands innovative technological solutions to support first responders in their efforts. This paper introduces the TRIFFID system, a comprehensive technical framework that integrates unmanned ground and aerial vehicles with advanced artificial intelligence functionalities to enhance disaster response capabilities across wildfires, urban floods, and post-earthquake search and rescue missions. By leveraging state-of-the-art autonomous navigation, semantic perception, and human-robot interaction technologies, TRIFFID provides a sophisticated system com- posed of the following key components: hybrid robotic platform, centralized ground station, custom communication infrastructure, and smartphone application. The defined research and development activities demonstrate how deep neural networks, knowledge graphs, and multimodal information fusion can enable robots to autonomously navigate and analyze disaster environ- ments, reducing personnel risks and accelerating response times. The proposed system enhances emergency response teams by providing advanced mission planning, safety monitoring, and adaptive task execution capabilities. Moreover, it ensures real- time situational awareness and operational support in complex and risky situations, facilitating rapid and precise information collection and coordinated actions.

As Time Goes By: Adding a Temporal Dimension Towards Resolving Delegations in Liquid Democracy

In recent years, the study of various models and questions related to Liquid Democracy has been of growing interest among the community of Computational Social Choice. A concern that has been raised, is that current academic literature focuses solely on static inputs, concealing a key characteristic of Liquid Democracy: the right for a voter to change her mind as time goes by, regarding her options of whether to vote herself or delegate her vote to other participants, till the final voting deadline. In real life, a period of extended deliberation preceding the election-day motivates voters to adapt their behaviour over time, either based on observations of the remaining electorate or on information acquired for the topic at hand. By adding a temporal dimension to Liquid Democracy, such adaptations can increase the number of possible delegation paths and reduce the loss of votes due to delegation cycles or delegating paths towards abstaining agents, ultimately enhancing participation. Our work takes a first step to integrate a time horizon into decision-making problems in Liquid Democracy systems. Our approach, via a computational complexity analysis, exploits concepts and tools from temporal graph theory which turn out to be convenient for our framework.

Computational Aspects of Conditional Minisum Approval Voting in Elections with Interdependent Issues

Approval voting provides a simple, practical framework for multi-issue elections, and the most representative example among such election rules is the classic Minisum approval voting rule. We consider a generalization of Minisum, introduced by the work of Barrot and Lang [2016], referred to as Conditional Minisum, where voters are also allowed to express dependencies between issues. The price we have to pay when we move to this higher level of expressiveness is that we end up with a computationally hard rule. Motivated by this, we focus on the computational aspects of Conditional Minisum, where progress has been rather scarce so far. We identify restrictions that concern the voters' dependencies and the value of an optimal solution, under which we provide the first multiplicative approximation algorithms for the problem. At the same time, by additionally requiring certain structural properties for the union of dependencies cast by the whole electorate, we obtain optimal efficient algorithms for well-motivated special cases. Overall, our work provides a better understanding on the complexity implications introduced by conditional voting.

Forward Looking Best-Response Multiplicative Weights Update Methods

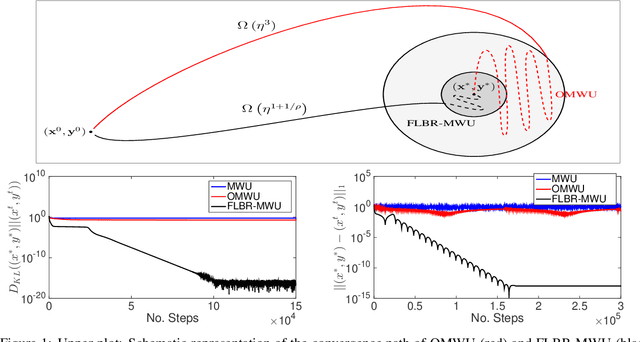
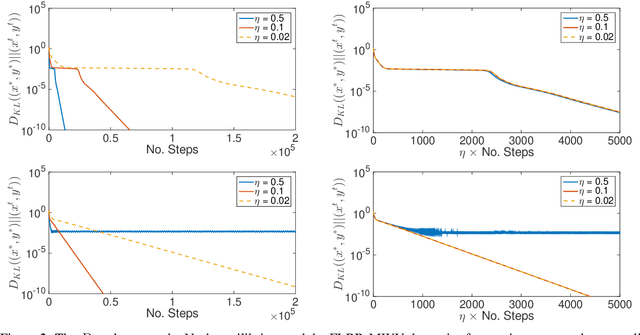
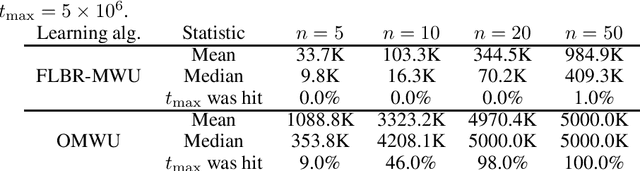
We propose a novel variant of the \emph{multiplicative weights update method} with forward-looking best-response strategies, that guarantees last-iterate convergence for \emph{zero-sum games} with a unique \emph{Nash equilibrium}. Particularly, we show that the proposed algorithm converges to an $\eta^{1/\rho}$-approximate Nash equilibrium, with $\rho > 1$, by decreasing the Kullback-Leibler divergence of each iterate by a rate of at least $\Omega(\eta^{1+\frac{1}{\rho}})$, for sufficiently small learning rate $\eta$. When our method enters a sufficiently small neighborhood of the solution, it becomes a contraction and converges to the Nash equilibrium of the game. Furthermore, we perform an experimental comparison with the recently proposed optimistic variant of the multiplicative weights update method, by \cite{Daskalakis2019LastIterateCZ}, which has also been proved to attain last-iterate convergence. Our findings reveal that our algorithm offers substantial gains both in terms of the convergence rate and the region of contraction relative to the previous approach.