Optimizing variational representations of divergences and accelerating their statistical estimation
Paper and Code
Jun 15, 2020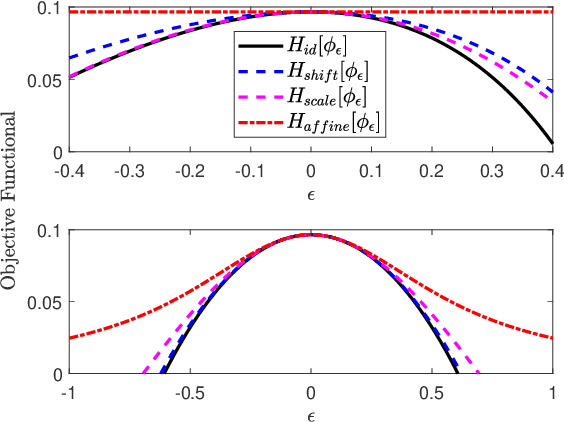
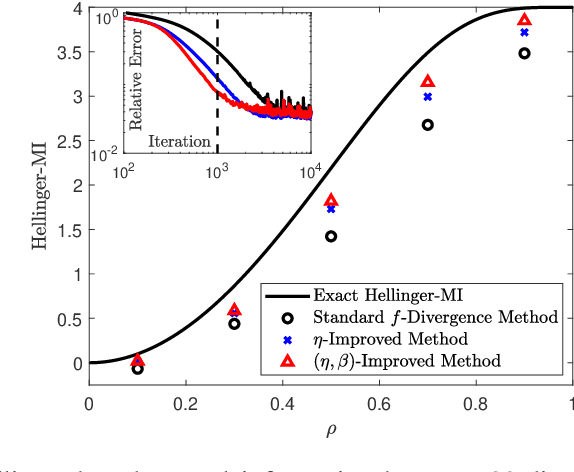
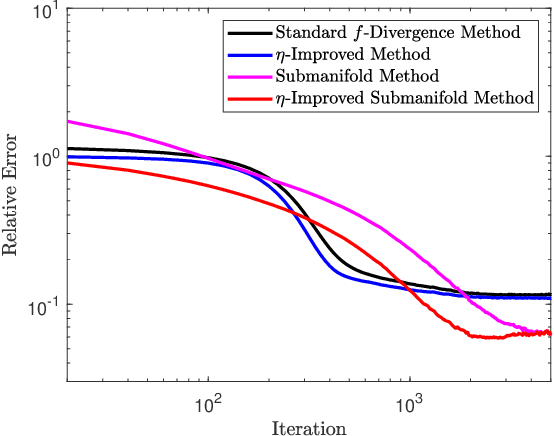
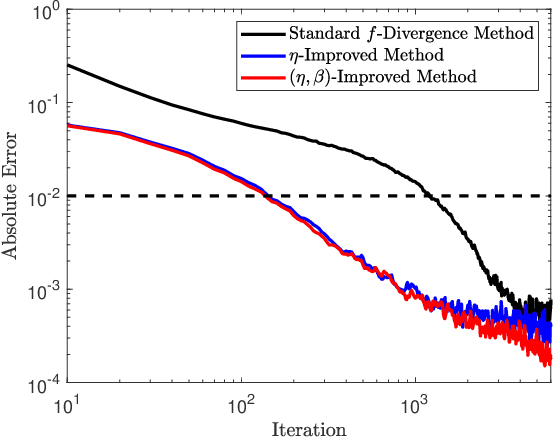
Variational representations of distances and divergences between high-dimensional probability distributions offer significant theoretical insights and practical advantages in numerous research areas. Recently, they have gained popularity in machine learning as a tractable and scalable approach for training probabilistic models and statistically differentiate between data distributions. Their advantages include: 1) They can be estimated from data. 2) Such representations can leverage the ability of neural networks to efficiently approximate optimal solutions in function spaces. However, a systematic and practical approach to improving the tightness of such variational formulas, and accordingly accelerate statistical learning and estimation from data, is currently lacking. Here we develop a systematic methodology for building new, tighter variational representations of divergences. Our approach relies on improved objective functionals constructed via an auxiliary optimization problem. Furthermore, the calculation of the functional Hessian of objective functionals unveils the local curvature differences around the common optimal variational solution; this allows us to quantify and order relative tightness gains between different variational representations. Finally, numerical simulations utilizing neural network optimization demonstrate that tighter representations can result in significantly faster learning and more accurate estimation of divergences in both synthetic and real datasets (of more than 700 dimensions), often accelerated by nearly an order of magnitude.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge