Concentration Inequalities for $(f,Γ)$-GANs

Generative adversarial networks (GANs) are unsupervised learning methods for training a generator distribution to produce samples that approximate those drawn from a target distribution. Many such methods can be formulated as minimization of a metric or divergence. Recent works have proven the statistical consistency of GANs that are based on integral probability metrics (IPMs), e.g., WGAN which is based on the 1-Wasserstein metric. IPMs are defined by optimizing a linear functional (difference of expectations) over a space of discriminators. A much larger class of GANs, which allow for the use of nonlinear objective functionals, can be constructed using $(f,\Gamma)$-divergences; these generalize and interpolate between IPMs and $f$-divergences (e.g., KL or $\alpha$-divergences). Instances of $(f,\Gamma)$-GANs have been shown to exhibit improved performance in a number of applications. In this work we study the statistical consistency of $(f,\Gamma)$-GANs for general $f$ and $\Gamma$. Specifically, we derive finite-sample concentration inequalities. These derivations require novel arguments due to nonlinearity of the objective functional. We demonstrate that our new results reduce to the known results for IPM-GANs in the appropriate limit while also significantly extending the domain of applicability of this theory.

Nonlinear denoising score matching for enhanced learning of structured distributions

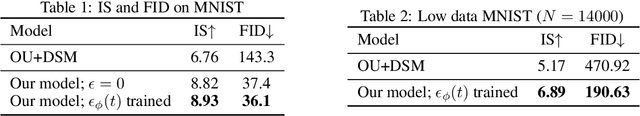
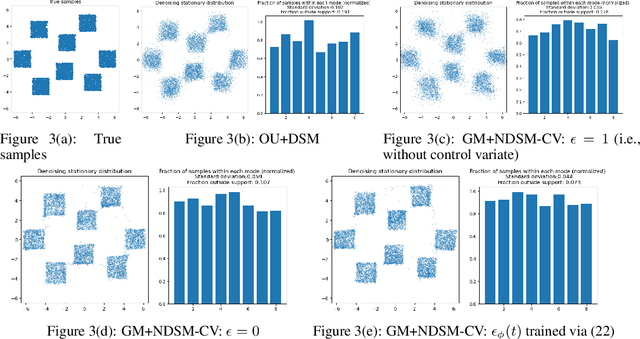
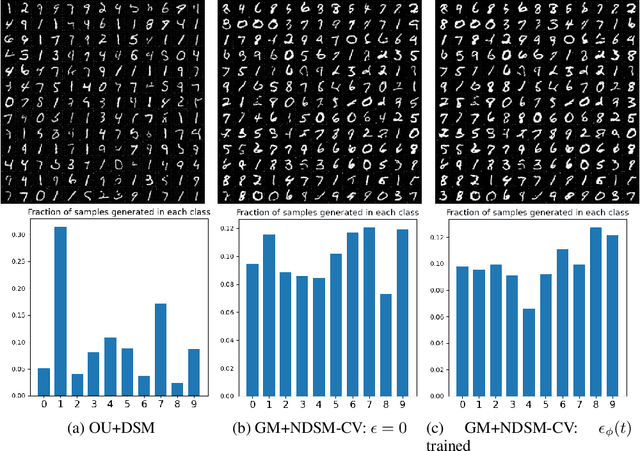
We present a novel method for training score-based generative models which uses nonlinear noising dynamics to improve learning of structured distributions. Generalizing to a nonlinear drift allows for additional structure to be incorporated into the dynamics, thus making the training better adapted to the data, e.g., in the case of multimodality or (approximate) symmetries. Such structure can be obtained from the data by an inexpensive preprocessing step. The nonlinear dynamics introduces new challenges into training which we address in two ways: 1) we develop a new nonlinear denoising score matching (NDSM) method, 2) we introduce neural control variates in order to reduce the variance of the NDSM training objective. We demonstrate the effectiveness of this method on several examples: a) a collection of low-dimensional examples, motivated by clustering in latent space, b) high-dimensional images, addressing issues with mode collapse, small training sets, and approximate symmetries, the latter being a challenge for methods based on equivariant neural networks, which require exact symmetries.

Adversarially Robust Deep Learning with Optimal-Transport-Regularized Divergences

We introduce the $ARMOR_D$ methods as novel approaches to enhancing the adversarial robustness of deep learning models. These methods are based on a new class of optimal-transport-regularized divergences, constructed via an infimal convolution between an information divergence and an optimal-transport (OT) cost. We use these as tools to enhance adversarial robustness by maximizing the expected loss over a neighborhood of distributions, a technique known as distributionally robust optimization. Viewed as a tool for constructing adversarial samples, our method allows samples to be both transported, according to the OT cost, and re-weighted, according to the information divergence. We demonstrate the effectiveness of our method on malware detection and image recognition applications and find that, to our knowledge, it outperforms existing methods at enhancing the robustness against adversarial attacks. $ARMOR_D$ yields the robustified accuracy of $98.29\%$ against $FGSM$ and $98.18\%$ against $PGD^{40}$ on the MNIST dataset, reducing the error rate by more than $19.7\%$ and $37.2\%$ respectively compared to prior methods. Similarly, in malware detection, a discrete (binary) data domain, $ARMOR_D$ improves the robustified accuracy under $rFGSM^{50}$ attack compared to the previous best-performing adversarial training methods by $37.0\%$ while lowering false negative and false positive rates by $51.1\%$ and $57.53\%$, respectively.

Function-space regularized Rényi divergences

We propose a new family of regularized R\'enyi divergences parametrized not only by the order $\alpha$ but also by a variational function space. These new objects are defined by taking the infimal convolution of the standard R\'enyi divergence with the integral probability metric (IPM) associated with the chosen function space. We derive a novel dual variational representation that can be used to construct numerically tractable divergence estimators. This representation avoids risk-sensitive terms and therefore exhibits lower variance, making it well-behaved when $\alpha>1$; this addresses a notable weakness of prior approaches. We prove several properties of these new divergences, showing that they interpolate between the classical R\'enyi divergences and IPMs. We also study the $\alpha\to\infty$ limit, which leads to a regularized worst-case-regret and a new variational representation in the classical case. Moreover, we show that the proposed regularized R\'enyi divergences inherit features from IPMs such as the ability to compare distributions that are not absolutely continuous, e.g., empirical measures and distributions with low-dimensional support. We present numerical results on both synthetic and real datasets, showing the utility of these new divergences in both estimation and GAN training applications; in particular, we demonstrate significantly reduced variance and improved training performance.

Structure-preserving GANs

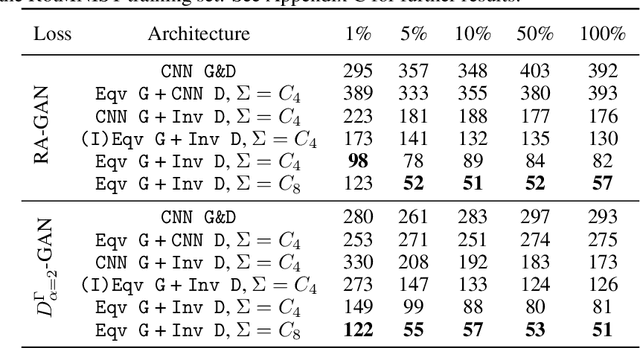
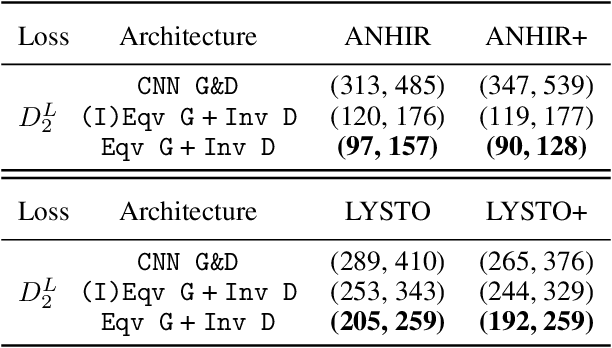
Generative adversarial networks (GANs), a class of distribution-learning methods based on a two-player game between a generator and a discriminator, can generally be formulated as a minmax problem based on the variational representation of a divergence between the unknown and the generated distributions. We introduce structure-preserving GANs as a data-efficient framework for learning distributions with additional structure such as group symmetry, by developing new variational representations for divergences. Our theory shows that we can reduce the discriminator space to its projection on the invariant discriminator space, using the conditional expectation with respect to the $\sigma$-algebra associated to the underlying structure. In addition, we prove that the discriminator space reduction must be accompanied by a careful design of structured generators, as flawed designs may easily lead to a catastrophic "mode collapse" of the learned distribution. We contextualize our framework by building symmetry-preserving GANs for distributions with intrinsic group symmetry, and demonstrate that both players, namely the equivariant generator and invariant discriminator, play important but distinct roles in the learning process. Empirical experiments and ablation studies across a broad range of data sets, including real-world medical imaging, validate our theory, and show our proposed methods achieve significantly improved sample fidelity and diversity -- almost an order of magnitude measured in Fr\'echet Inception Distance -- especially in the small data regime.

$(f,Γ)$-Divergences: Interpolating between $f$-Divergences and Integral Probability Metrics

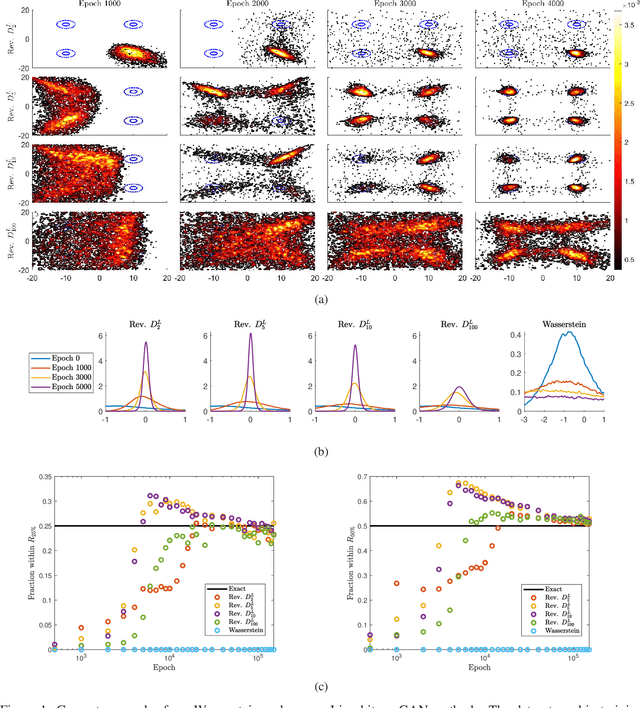
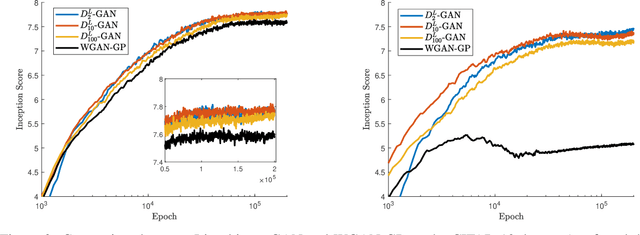
We develop a general framework for constructing new information-theoretic divergences that rigorously interpolate between $f$-divergences and integral probability metrics (IPMs), such as the Wasserstein distance. These new divergences inherit features from IPMs, such as the ability to compare distributions which are not absolute continuous, as well as from $f$-divergences, for instance the strict concavity of their variational representations and the ability to compare heavy-tailed distributions. When combined, these features establish a divergence with improved convergence and estimation properties for statistical learning applications. We demonstrate their use in the training of generative adversarial networks (GAN) for heavy-tailed data and also show they can provide improved performance over gradient-penalized Wasserstein GAN in image generation.

A Variational Formula for Rényi Divergences

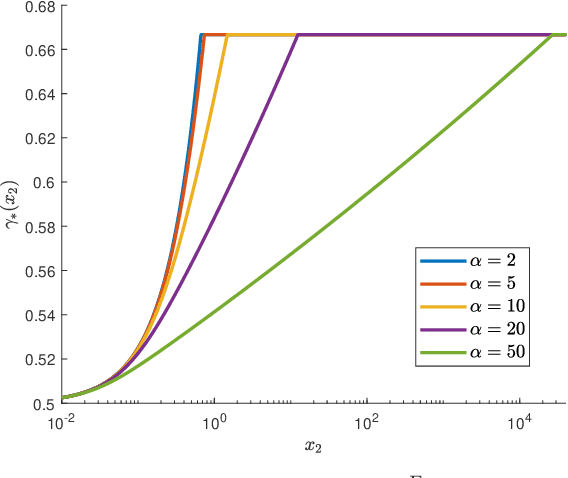
We derive a new variational formula for the R\'enyi family of divergences, $R_\alpha(Q\|P)$, generalizing the classical Donsker-Varadhan variational formula for the Kullback-Leibler divergence. The objective functional in this new variational representation is expressed in terms of expectations under $Q$ and $P$, and hence can be estimated using samples from the two distributions. We illustrate the utility of such a variational formula by constructing neural-network estimators for the R\'enyi divergences.

Optimizing variational representations of divergences and accelerating their statistical estimation

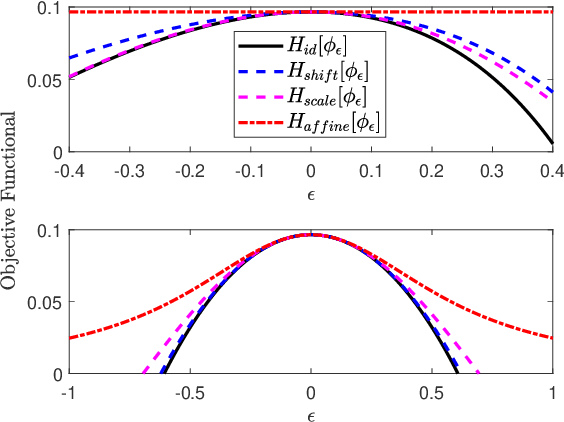
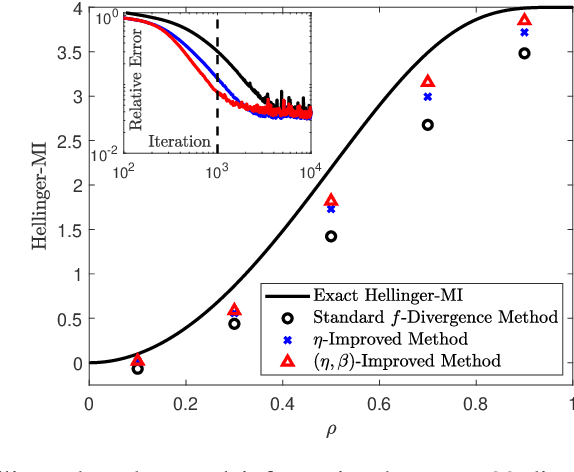
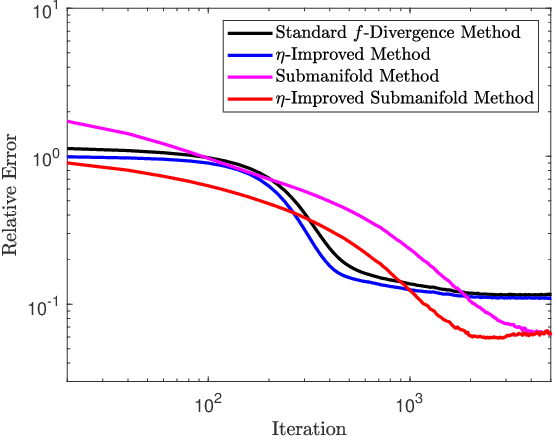
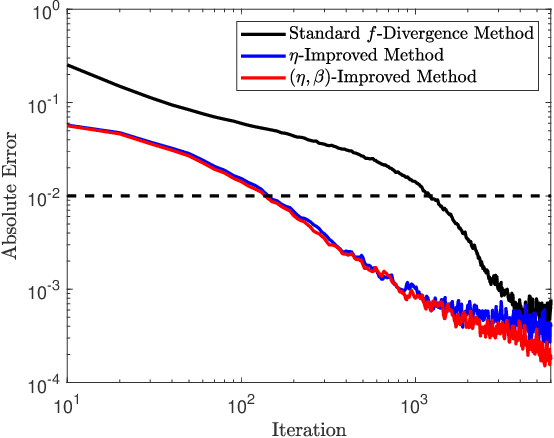
Variational representations of distances and divergences between high-dimensional probability distributions offer significant theoretical insights and practical advantages in numerous research areas. Recently, they have gained popularity in machine learning as a tractable and scalable approach for training probabilistic models and statistically differentiate between data distributions. Their advantages include: 1) They can be estimated from data. 2) Such representations can leverage the ability of neural networks to efficiently approximate optimal solutions in function spaces. However, a systematic and practical approach to improving the tightness of such variational formulas, and accordingly accelerate statistical learning and estimation from data, is currently lacking. Here we develop a systematic methodology for building new, tighter variational representations of divergences. Our approach relies on improved objective functionals constructed via an auxiliary optimization problem. Furthermore, the calculation of the functional Hessian of objective functionals unveils the local curvature differences around the common optimal variational solution; this allows us to quantify and order relative tightness gains between different variational representations. Finally, numerical simulations utilizing neural network optimization demonstrate that tighter representations can result in significantly faster learning and more accurate estimation of divergences in both synthetic and real datasets (of more than 700 dimensions), often accelerated by nearly an order of magnitude.