A Variational Formula for Rényi Divergences
Paper and Code
Jul 07, 2020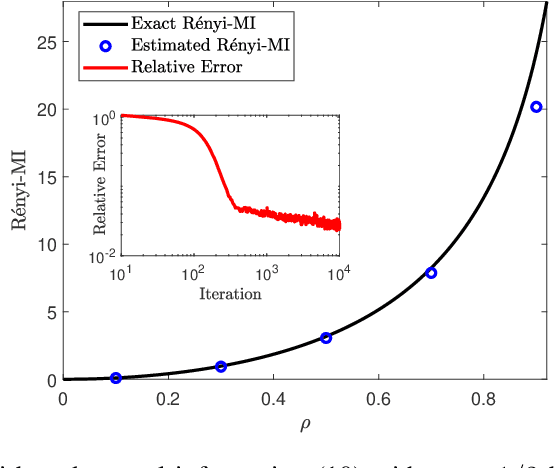

We derive a new variational formula for the R\'enyi family of divergences, $R_\alpha(Q\|P)$, generalizing the classical Donsker-Varadhan variational formula for the Kullback-Leibler divergence. The objective functional in this new variational representation is expressed in terms of expectations under $Q$ and $P$, and hence can be estimated using samples from the two distributions. We illustrate the utility of such a variational formula by constructing neural-network estimators for the R\'enyi divergences.
* 11 pages, 2 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge