Function-space regularized Rényi divergences

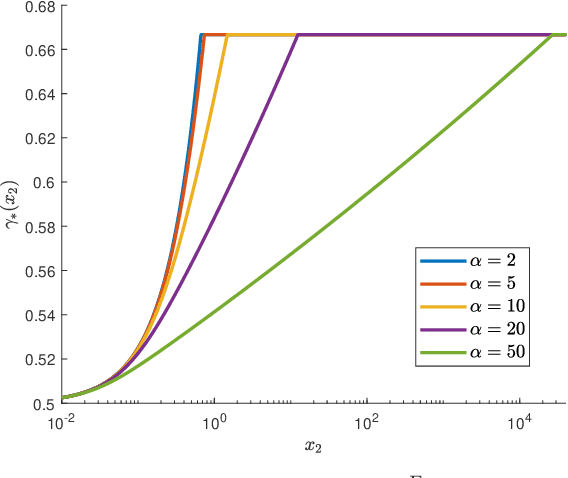
We propose a new family of regularized R\'enyi divergences parametrized not only by the order $\alpha$ but also by a variational function space. These new objects are defined by taking the infimal convolution of the standard R\'enyi divergence with the integral probability metric (IPM) associated with the chosen function space. We derive a novel dual variational representation that can be used to construct numerically tractable divergence estimators. This representation avoids risk-sensitive terms and therefore exhibits lower variance, making it well-behaved when $\alpha>1$; this addresses a notable weakness of prior approaches. We prove several properties of these new divergences, showing that they interpolate between the classical R\'enyi divergences and IPMs. We also study the $\alpha\to\infty$ limit, which leads to a regularized worst-case-regret and a new variational representation in the classical case. Moreover, we show that the proposed regularized R\'enyi divergences inherit features from IPMs such as the ability to compare distributions that are not absolutely continuous, e.g., empirical measures and distributions with low-dimensional support. We present numerical results on both synthetic and real datasets, showing the utility of these new divergences in both estimation and GAN training applications; in particular, we demonstrate significantly reduced variance and improved training performance.

$(f,Γ)$-Divergences: Interpolating between $f$-Divergences and Integral Probability Metrics

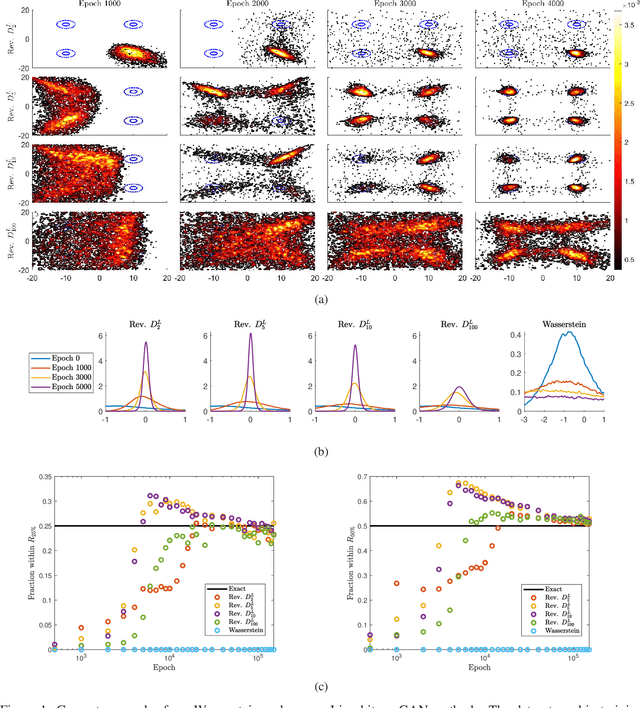
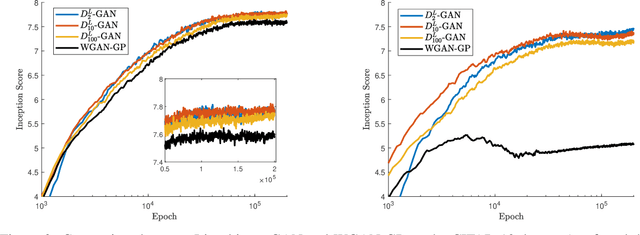
We develop a general framework for constructing new information-theoretic divergences that rigorously interpolate between $f$-divergences and integral probability metrics (IPMs), such as the Wasserstein distance. These new divergences inherit features from IPMs, such as the ability to compare distributions which are not absolute continuous, as well as from $f$-divergences, for instance the strict concavity of their variational representations and the ability to compare heavy-tailed distributions. When combined, these features establish a divergence with improved convergence and estimation properties for statistical learning applications. We demonstrate their use in the training of generative adversarial networks (GAN) for heavy-tailed data and also show they can provide improved performance over gradient-penalized Wasserstein GAN in image generation.

A Variational Formula for Rényi Divergences

We derive a new variational formula for the R\'enyi family of divergences, $R_\alpha(Q\|P)$, generalizing the classical Donsker-Varadhan variational formula for the Kullback-Leibler divergence. The objective functional in this new variational representation is expressed in terms of expectations under $Q$ and $P$, and hence can be estimated using samples from the two distributions. We illustrate the utility of such a variational formula by constructing neural-network estimators for the R\'enyi divergences.