$(f,Γ)$-Divergences: Interpolating between $f$-Divergences and Integral Probability Metrics

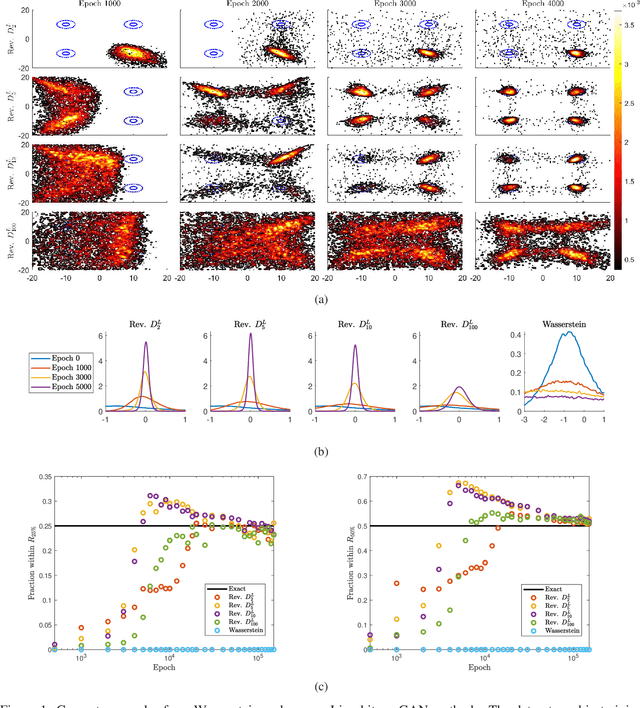
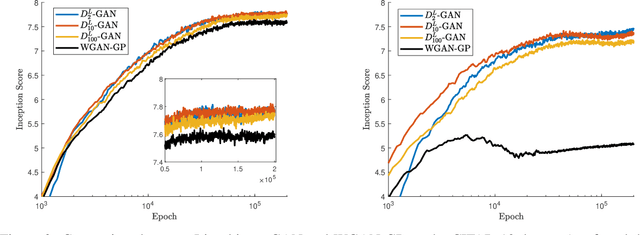
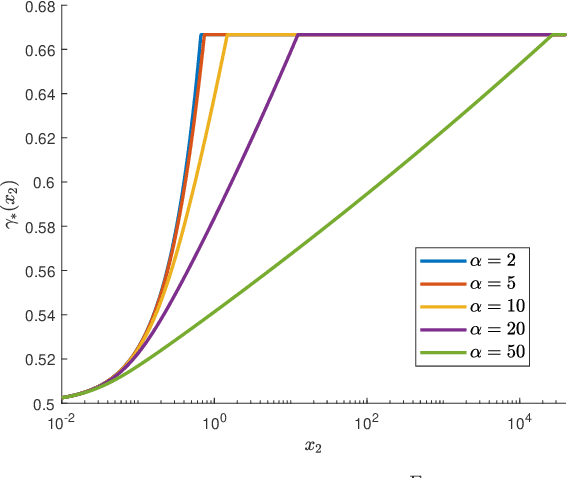
We develop a general framework for constructing new information-theoretic divergences that rigorously interpolate between $f$-divergences and integral probability metrics (IPMs), such as the Wasserstein distance. These new divergences inherit features from IPMs, such as the ability to compare distributions which are not absolute continuous, as well as from $f$-divergences, for instance the strict concavity of their variational representations and the ability to compare heavy-tailed distributions. When combined, these features establish a divergence with improved convergence and estimation properties for statistical learning applications. We demonstrate their use in the training of generative adversarial networks (GAN) for heavy-tailed data and also show they can provide improved performance over gradient-penalized Wasserstein GAN in image generation.