Microstructures and Accuracy of Graph Recall by Large Language Models

Graphs data is crucial for many applications, and much of it exists in the relations described in textual format. As a result, being able to accurately recall and encode a graph described in earlier text is a basic yet pivotal ability that LLMs need to demonstrate if they are to perform reasoning tasks that involve graph-structured information. Human performance at graph recall has been studied by cognitive scientists for decades, and has been found to often exhibit certain structural patterns of bias that align with human handling of social relationships. To date, however, we know little about how LLMs behave in analogous graph recall tasks: do their recalled graphs also exhibit certain biased patterns, and if so, how do they compare with humans and affect other graph reasoning tasks? In this work, we perform the first systematical study of graph recall by LLMs, investigating the accuracy and biased microstructures (local structural patterns) in their recall. We find that LLMs not only underperform often in graph recall, but also tend to favor more triangles and alternating 2-paths. Moreover, we find that more advanced LLMs have a striking dependence on the domain that a real-world graph comes from -- by yielding the best recall accuracy when the graph is narrated in a language style consistent with its original domain.

From Graphs to Hypergraphs: Hypergraph Projection and its Remediation

We study the implications of the modeling choice to use a graph, instead of a hypergraph, to represent real-world interconnected systems whose constituent relationships are of higher order by nature. Such a modeling choice typically involves an underlying projection process that maps the original hypergraph onto a graph, and is common in graph-based analysis. While hypergraph projection can potentially lead to loss of higher-order relations, there exists very limited studies on the consequences of doing so, as well as its remediation. This work fills this gap by doing two things: (1) we develop analysis based on graph and set theory, showing two ubiquitous patterns of hyperedges that are root to structural information loss in all hypergraph projections; we also quantify the combinatorial impossibility of recovering the lost higher-order structures if no extra help is provided; (2) we still seek to recover the lost higher-order structures in hypergraph projection, and in light of (1)'s findings we propose to relax the problem into a learning-based setting. Under this setting, we develop a learning-based hypergraph reconstruction method based on an important statistic of hyperedge distributions that we find. Our reconstruction method is evaluated on 8 real-world datasets under different settings, and exhibits consistently good performance. We also demonstrate benefits of the reconstructed hypergraphs via use cases of protein rankings and link predictions.

Supervised Hypergraph Reconstruction

We study an issue commonly seen with graph data analysis: many real-world complex systems involving high-order interactions are best encoded by hypergraphs; however, their datasets often end up being published or studied only in the form of their projections (with dyadic edges). To understand this issue, we first establish a theoretical framework to characterize this issue's implications and worst-case scenarios. The analysis motivates our formulation of the new task, supervised hypergraph reconstruction: reconstructing a real-world hypergraph from its projected graph, with the help of some existing knowledge of the application domain. To reconstruct hypergraph data, we start by analyzing hyperedge distributions in the projection, based on which we create a framework containing two modules: (1) to handle the enormous search space of potential hyperedges, we design a sampling strategy with efficacy guarantees that significantly narrows the space to a smaller set of candidates; (2) to identify hyperedges from the candidates, we further design a hyperedge classifier in two well-working variants that capture structural features in the projection. Extensive experiments validate our claims, approach, and extensions. Remarkably, our approach outperforms all baselines by an order of magnitude in accuracy on hard datasets. Our code and data can be downloaded from bit.ly/SHyRe.

Algorithm and System Co-design for Efficient Subgraph-based Graph Representation Learning

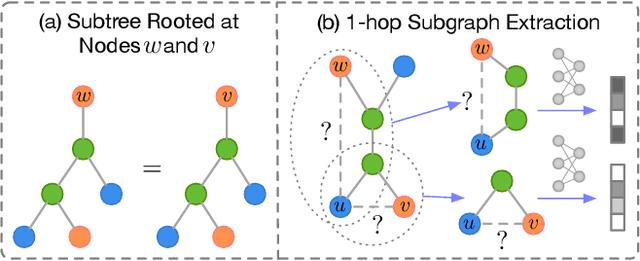
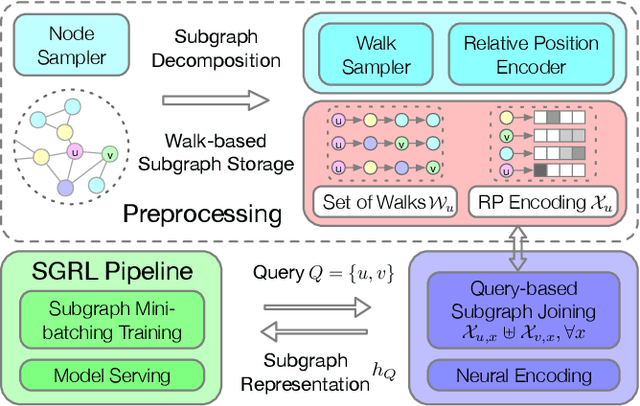
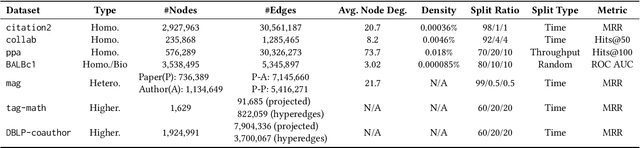
Subgraph-based graph representation learning (SGRL) has been recently proposed to deal with some fundamental challenges encountered by canonical graph neural networks (GNNs), and has demonstrated advantages in many important data science applications such as link, relation and motif prediction. However, current SGRL approaches suffer from a scalability issue since they require extracting subgraphs for each training and testing query. Recent solutions that scale up canonical GNNs may not apply to SGRL. Here, we propose a novel framework SUREL for scalable SGRL by co-designing the learning algorithm and its system support. SUREL adopts walk-based decomposition of subgraphs and reuses the walks to form subgraphs, which substantially reduces the redundancy of subgraph extraction and supports parallel computation. Experiments over seven homogeneous, heterogeneous and higher-order graphs with millions of nodes and edges demonstrate the effectiveness and scalability of SUREL. In particular, compared to SGRL baselines, SUREL achieves 10$\times$ speed-up with comparable or even better prediction performance; while compared to canonical GNNs, SUREL achieves 50% prediction accuracy improvement. SUREL is also applied to the brain vessel prediction task. SUREL significantly outperforms the state-of-the-art baseline in both prediction accuracy and efficiency.

Inductive Representation Learning in Temporal Networks via Causal Anonymous Walks

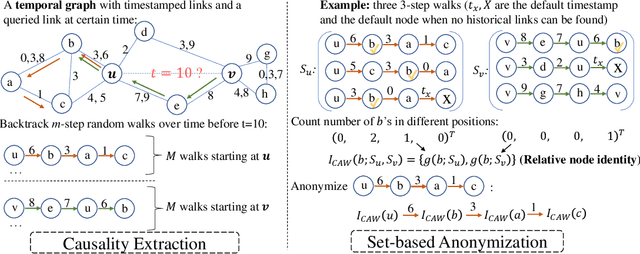
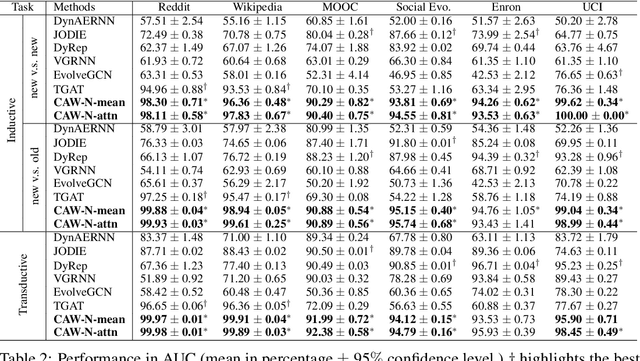
Temporal networks serve as abstractions of many real-world dynamic systems. These networks typically evolve according to certain laws, such as the law of triadic closure, which is universal in social networks. Inductive representation learning of temporal networks should be able to capture such laws and further be applied to systems that follow the same laws but have not been unseen during the training stage. Previous works in this area depend on either network node identities or rich edge attributes and typically fail to extract these laws. Here, we propose Causal Anonymous Walks (CAWs) to inductively represent a temporal network. CAWs are extracted by temporal random walks and work as automatic retrieval of temporal network motifs to represent network dynamics while avoiding the time-consuming selection and counting of those motifs. CAWs adopt a novel anonymization strategy that replaces node identities with the hitting counts of the nodes based on a set of sampled walks to keep the method inductive, and simultaneously establish the correlation between motifs. We further propose a neural-network model CAW-N to encode CAWs, and pair it with a CAW sampling strategy with constant memory and time cost to support online training and inference. CAW-N is evaluated to predict links over 6 real temporal networks and uniformly outperforms previous SOTA methods by averaged 15% AUC gain in the inductive setting. CAW-N also outperforms previous methods in 5 out of the 6 networks in the transductive setting.

Revisiting graph neural networks and distance encoding from a practical view

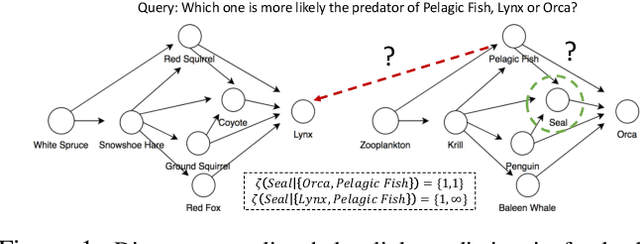
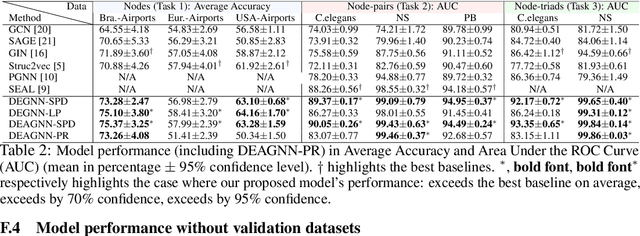
Graph neural networks (GNNs) are widely used in the applications based on graph structured data, such as node classification and link prediction. However, GNNs are often used as a black-box tool and rarely get in-depth investigated regarding whether they fit certain applications that may have various properties. A recently proposed technique distance encoding (DE) (Li et al. 2020) magically makes GNNs work well in many applications, including node classification and link prediction. The theory provided in (Li et al. 2020) supports DE by proving that DE improves the representation power of GNNs. However, it is not obvious how the theory assists the applications accordingly. Here, we revisit GNNs and DE from a more practical point of view. We want to explain how DE makes GNNs fit for node classification and link prediction. Specifically, for link prediction, DE can be viewed as a way to establish correlations between a pair of node representations. For node classification, the problem becomes more complicated as different classification tasks may hold node labels that indicate different physical meanings. We focus on the most widely-considered node classification scenarios and categorize the node labels into two types, community type and structure type, and then analyze different mechanisms that GNNs adopt to predict these two types of labels. We also run extensive experiments to compare eight different configurations of GNNs paired with DE to predict node labels over eight real-world graphs. The results demonstrate the uniform effectiveness of DE to predict structure-type labels. Lastly, we reach three pieces of conclusions on how to use GNNs and DE properly in tasks of node classification.

Distance Encoding -- Design Provably More Powerful Graph Neural Networks for Structural Representation Learning

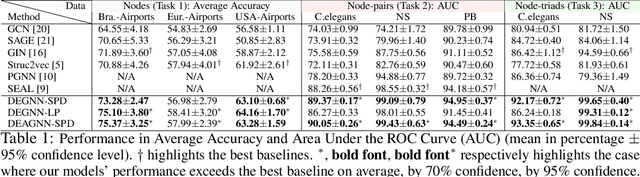
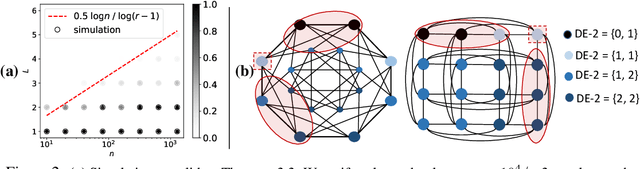
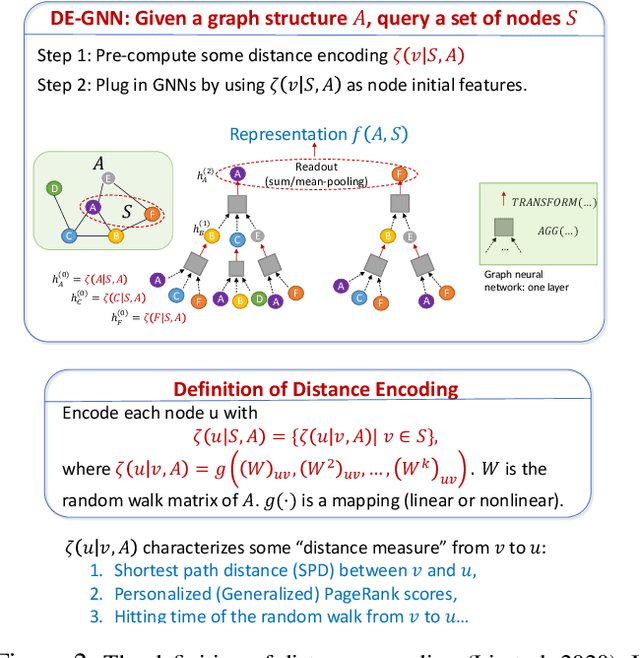
Learning structural representations of node sets from graph-structured data is crucial for applications ranging from node-role discovery to link prediction and molecule classification. Graph Neural Networks (GNNs) have achieved great success in structural representation learning. However, most GNNs are limited by the 1-Weisfeiler-Lehman (WL) test and thus possible to generate identical representation for structures and graphs that are actually different. More powerful GNNs, proposed recently by mimicking higher-order-WL tests, only focus on entire-graph representations and cannot utilize sparsity of the graph structure to be computationally efficient. Here we propose a general class of structure-related features, termed Distance Encoding (DE), to assist GNNs in representing node sets with arbitrary sizes with strictly more expressive power than the 1-WL test. DE essentially captures the distance between the node set whose representation is to be learnt and each node in the graph, which includes important graph-related measures such as shortest-path-distance and generalized PageRank scores. We propose two general frameworks for GNNs to use DEs (1) as extra node attributes and (2) further as controllers of message aggregation in GNNs. Both frameworks may still utilize the sparse structure to keep scalability to process large graphs. In theory, we prove that these two frameworks can distinguish node sets embedded in almost all regular graphs where traditional GNNs always fail. We also rigorously analyze their limitations. Empirically, we evaluate these two frameworks on node structural roles prediction, link prediction and triangle prediction over six real networks. The results show that our models outperform GNNs without DEs by up-to 15% improvement in average accuracy and AUC. Our models also significantly outperform other SOTA baselines particularly designed for those tasks.

Transfer Learning using Representation Learning in Massive Open Online Courses

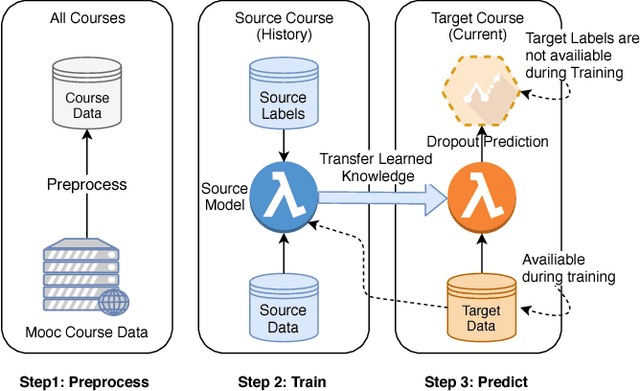
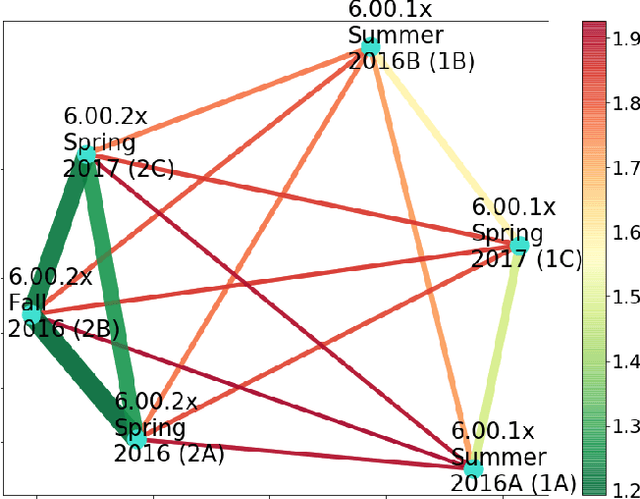
In a Massive Open Online Course (MOOC), predictive models of student behavior can support multiple aspects of learning, including instructor feedback and timely intervention. Ongoing courses, when the student outcomes are yet unknown, must rely on models trained from the historical data of previously offered courses. It is possible to transfer models, but they often have poor prediction performance. One reason is features that inadequately represent predictive attributes common to both courses. We present an automated transductive transfer learning approach that addresses this issue. It relies on problem-agnostic, temporal organization of the MOOC clickstream data, where, for each student, for multiple courses, a set of specific MOOC event types is expressed for each time unit. It consists of two alternative transfer methods based on representation learning with auto-encoders: a passive approach using transductive principal component analysis and an active approach that uses a correlation alignment loss term. With these methods, we investigate the transferability of dropout prediction across similar and dissimilar MOOCs and compare with known methods. Results show improved model transferability and suggest that the methods are capable of automatically learning a feature representation that expresses common predictive characteristics of MOOCs.

Using Detailed Access Trajectories for Learning Behavior Analysis

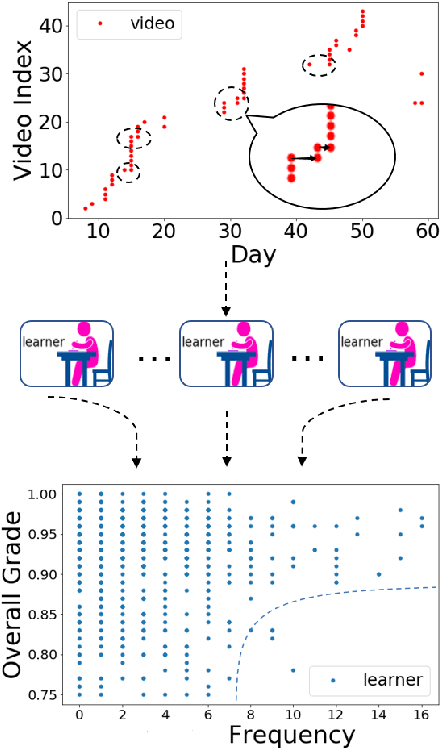
Student learning activity in MOOCs can be viewed from multiple perspectives. We present a new organization of MOOC learner activity data at a resolution that is in between the fine granularity of the clickstream and coarse organizations that count activities, aggregate students or use long duration time units. A detailed access trajectory (DAT) consists of binary values and is two dimensional with one axis that is a time series, e.g. days and the other that is a chronologically ordered list of a MOOC component type's instances, e.g. videos in instructional order. Most popular MOOC platforms generate data that can be organized as detailed access trajectories (DATs).We explore the value of DATs by conducting four empirical mini-studies. Our studies suggest DATs contain rich information about students' learning behaviors and facilitate MOOC learning analyses.