Equivariant Hypergraph Diffusion Neural Operators

Hypergraph neural networks (HNNs) using neural networks to encode hypergraphs provide a promising way to model higher-order relations in data and further solve relevant prediction tasks built upon such higher-order relations. However, higher-order relations in practice contain complex patterns and are often highly irregular. So, it is often challenging to design an HNN that suffices to express those relations while keeping computational efficiency. Inspired by hypergraph diffusion algorithms, this work proposes a new HNN architecture named ED-HNN, which provably represents any continuous equivariant hypergraph diffusion operators that can model a wide range of higher-order relations. ED-HNN can be implemented efficiently by combining star expansions of hypergraphs with standard message passing neural networks. ED-HNN further shows great superiority in processing heterophilic hypergraphs and constructing deep models. We evaluate ED-HNN for node classification on nine real-world hypergraph datasets. ED-HNN uniformly outperforms the best baselines over these nine datasets and achieves more than 2\%$\uparrow$ in prediction accuracy over four datasets therein.

Neural Higher-order Pattern (Motif) Prediction in Temporal Networks

Dynamic systems that consist of a set of interacting elements can be abstracted as temporal networks. Recently, higher-order patterns that involve multiple interacting nodes have been found crucial to indicate domain-specific laws of different temporal networks. This posts us the challenge of designing more sophisticated hypergraph models for these higher-order patterns and the associated new learning algorithms. Here, we propose the first model, named HIT, for higher-order pattern prediction in temporal hypergraphs. Particularly, we focus on predicting three types of common but important interaction patterns involving three interacting elements in temporal networks, which could be extended to even higher-order patterns. HIT extracts the structural representation of a node triplet of interest on the temporal hypergraph and uses it to tell what type of, when, and why the interaction expansion could happen in this triplet. HIT could achieve significant improvement(averaged 20% AUC gain to identify the interaction type, uniformly more accurate time estimation) compared to both heuristic and other neural-network-based baselines on 5 real-world large temporal hypergraphs. Moreover, HIT provides a certain degree of interpretability by identifying the most discriminatory structural features on the temporal hypergraphs for predicting different higher-order patterns.

Inductive Representation Learning in Temporal Networks via Causal Anonymous Walks

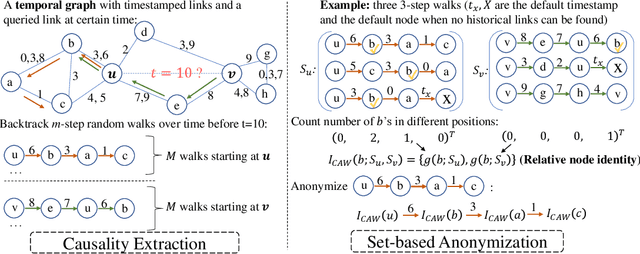
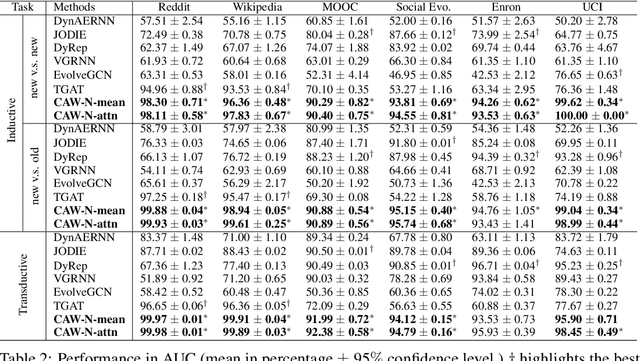
Temporal networks serve as abstractions of many real-world dynamic systems. These networks typically evolve according to certain laws, such as the law of triadic closure, which is universal in social networks. Inductive representation learning of temporal networks should be able to capture such laws and further be applied to systems that follow the same laws but have not been unseen during the training stage. Previous works in this area depend on either network node identities or rich edge attributes and typically fail to extract these laws. Here, we propose Causal Anonymous Walks (CAWs) to inductively represent a temporal network. CAWs are extracted by temporal random walks and work as automatic retrieval of temporal network motifs to represent network dynamics while avoiding the time-consuming selection and counting of those motifs. CAWs adopt a novel anonymization strategy that replaces node identities with the hitting counts of the nodes based on a set of sampled walks to keep the method inductive, and simultaneously establish the correlation between motifs. We further propose a neural-network model CAW-N to encode CAWs, and pair it with a CAW sampling strategy with constant memory and time cost to support online training and inference. CAW-N is evaluated to predict links over 6 real temporal networks and uniformly outperforms previous SOTA methods by averaged 15% AUC gain in the inductive setting. CAW-N also outperforms previous methods in 5 out of the 6 networks in the transductive setting.