Xiyu Zhai
SceneGen: Generative Contextual Scene Augmentation using Scene Graph Priors
Sep 30, 2020


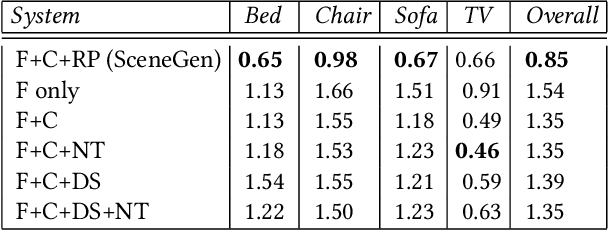
Abstract:Spatial computing experiences are constrained by the real-world surroundings of the user. In such experiences, augmenting virtual objects to existing scenes require a contextual approach, where geometrical conflicts are avoided, and functional and plausible relationships to other objects are maintained in the target environment. Yet, due to the complexity and diversity of user environments, automatically calculating ideal positions of virtual content that is adaptive to the context of the scene is considered a challenging task. Motivated by this problem, in this paper we introduce SceneGen, a generative contextual augmentation framework that predicts virtual object positions and orientations within existing scenes. SceneGen takes a semantically segmented scene as input, and outputs positional and orientational probability maps for placing virtual content. We formulate a novel spatial Scene Graph representation, which encapsulates explicit topological properties between objects, object groups, and the room. We believe providing explicit and intuitive features plays an important role in informative content creation and user interaction of spatial computing settings, a quality that is not captured in implicit models. We use kernel density estimation (KDE) to build a multivariate conditional knowledge model trained using prior spatial Scene Graphs extracted from real-world 3D scanned data. To further capture orientational properties, we develop a fast pose annotation tool to extend current real-world datasets with orientational labels. Finally, to demonstrate our system in action, we develop an Augmented Reality application, in which objects can be contextually augmented in real-time.
On the Risk of Minimum-Norm Interpolants and Restricted Lower Isometry of Kernels
Aug 27, 2019Abstract:We study the risk of minimum-norm interpolants of data in a Reproducing Kernel Hilbert Space where kernel is defined as a function of the inner product. Our upper bounds on the risk are of a multiple-descent shape for the various scalings of d = n^\alpha, \alpha\in(0,1), for the input dimension d and sample size n. At the heart of our analysis is a study of spectral properties of the random kernel matrix restricted to a filtration of eigen-spaces of the population covariance operator. Since gradient flow on appropriately initialized wide neural networks converges to a minimum-norm interpolant, the analysis also yields estimation guarantees for these models.
Near Optimal Stratified Sampling
Jul 26, 2019

Abstract:The performance of a machine learning system is usually evaluated by using i.i.d.\ observations with true labels. However, acquiring ground truth labels is expensive, while obtaining unlabeled samples may be cheaper. Stratified sampling can be beneficial in such settings and can reduce the number of true labels required without compromising the evaluation accuracy. Stratified sampling exploits statistical properties (e.g., variance) across strata of the unlabeled population, though usually under the unrealistic assumption that these properties are known. We propose two new algorithms that simultaneously estimate these properties and optimize the evaluation accuracy. We construct a lower bound to show the proposed algorithms (to log-factors) are rate optimal. Experiments on synthetic and real data show the reduction in label complexity that is enabled by our algorithms.
Consistency of Interpolation with Laplace Kernels is a High-Dimensional Phenomenon
Dec 28, 2018Abstract:We show that minimum-norm interpolation in the Reproducing Kernel Hilbert Space corresponding to the Laplace kernel is not consistent if input dimension is constant. The lower bound holds for any choice of kernel bandwidth, even if selected based on data. The result supports the empirical observation that minimum-norm interpolation (that is, exact fit to training data) in RKHS generalizes well for some high-dimensional datasets, but not for low-dimensional ones.
Gradient Descent Finds Global Minima of Deep Neural Networks
Nov 30, 2018Abstract:Gradient descent finds a global minimum in training deep neural networks despite the objective function being non-convex. The current paper proves gradient descent achieves zero training loss in polynomial time for a deep over-parameterized neural network with residual connections (ResNet). Our analysis relies on the particular structure of the Gram matrix induced by the neural network architecture. This structure allows us to show the Gram matrix is stable throughout the training process and this stability implies the global optimality of the gradient descent algorithm. We further extend our analysis to deep residual convolutional neural networks and obtain a similar convergence result.
How Many Samples are Needed to Learn a Convolutional Neural Network?
May 21, 2018



Abstract:A widespread folklore for explaining the success of convolutional neural network (CNN) is that CNN is a more compact representation than the fully connected neural network (FNN) and thus requires fewer samples for learning. We initiate the study of rigorously characterizing the sample complexity of learning convolutional neural networks. We show that for learning an $m$-dimensional convolutional filter with linear activation acting on a $d$-dimensional input, the sample complexity of achieving population prediction error of $\epsilon$ is $\widetilde{O} (m/\epsilon^2)$, whereas its FNN counterpart needs at least $\Omega(d/\epsilon^2)$ samples. Since $m \ll d$, this result demonstrates the advantage of using CNN. We further consider the sample complexity of learning a one-hidden-layer CNN with linear activation where both the $m$-dimensional convolutional filter and the $r$-dimensional output weights are unknown. For this model, we show the sample complexity is $\widetilde{O}\left((m+r)/\epsilon^2\right)$ when the ratio between the stride size and the filter size is a constant. For both models, we also present lower bounds showing our sample complexities are tight up to logarithmic factors. Our main tools for deriving these results are localized empirical process and a new lemma characterizing the convolutional structure. We believe these tools may inspire further developments in understanding CNN.
Generalization Bounds of SGLD for Non-convex Learning: Two Theoretical Viewpoints
Jul 19, 2017
Abstract:Algorithm-dependent generalization error bounds are central to statistical learning theory. A learning algorithm may use a large hypothesis space, but the limited number of iterations controls its model capacity and generalization error. The impacts of stochastic gradient methods on generalization error for non-convex learning problems not only have important theoretical consequences, but are also critical to generalization errors of deep learning. In this paper, we study the generalization errors of Stochastic Gradient Langevin Dynamics (SGLD) with non-convex objectives. Two theories are proposed with non-asymptotic discrete-time analysis, using Stability and PAC-Bayesian results respectively. The stability-based theory obtains a bound of $O\left(\frac{1}{n}L\sqrt{\beta T_k}\right)$, where $L$ is uniform Lipschitz parameter, $\beta$ is inverse temperature, and $T_k$ is aggregated step sizes. For PAC-Bayesian theory, though the bound has a slower $O(1/\sqrt{n})$ rate, the contribution of each step is shown with an exponentially decaying factor by imposing $\ell^2$ regularization, and the uniform Lipschitz constant is also replaced by actual norms of gradients along trajectory. Our bounds have no implicit dependence on dimensions, norms or other capacity measures of parameter, which elegantly characterizes the phenomenon of "Fast Training Guarantees Generalization" in non-convex settings. This is the first algorithm-dependent result with reasonable dependence on aggregated step sizes for non-convex learning, and has important implications to statistical learning aspects of stochastic gradient methods in complicated models such as deep learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge