Explainable Censored Learning: Finding Critical Features with Long Term Prognostic Values for Survival Prediction

Interpreting critical variables involved in complex biological processes related to survival time can help understand prediction from survival models, evaluate treatment efficacy, and develop new therapies for patients. Currently, the predictive results of deep learning (DL)-based models are better than or as good as standard survival methods, they are often disregarded because of their lack of transparency and little interpretability, which is crucial to their adoption in clinical applications. In this paper, we introduce a novel, easily deployable approach, called EXplainable CEnsored Learning (EXCEL), to iteratively exploit critical variables and simultaneously implement (DL) model training based on these variables. First, on a toy dataset, we illustrate the principle of EXCEL; then, we mathematically analyze our proposed method, and we derive and prove tight generalization error bounds; next, on two semi-synthetic datasets, we show that EXCEL has good anti-noise ability and stability; finally, we apply EXCEL to a variety of real-world survival datasets including clinical data and genetic data, demonstrating that EXCEL can effectively identify critical features and achieve performance on par with or better than the original models. It is worth pointing out that EXCEL is flexibly deployed in existing or emerging models for explainable survival data in the presence of right censoring.

PRIME: Uncovering Circadian Oscillation Patterns and Associations with AD in Untimed Genome-wide Gene Expression across Multiple Brain Regions

The disruption of circadian rhythm is a cardinal symptom for Alzheimer's disease (AD) patients. The full circadian rhythm orchestration of gene expression in the human brain and its inherent associations with AD remain largely unknown. We present a novel comprehensive approach, PRIME, to detect and analyze rhythmic oscillation patterns in untimed high-dimensional gene expression data across multiple datasets. To demonstrate the utility of PRIME, firstly, we validate it by a time course expression dataset from mouse liver as a cross-species and cross-organ validation. Then, we apply it to study oscillation patterns in untimed genome-wide gene expression from 19 human brain regions of controls and AD patients. Our findings reveal clear, synchronized oscillation patterns in 15 pairs of brain regions of control, while these oscillation patterns either disappear or dim for AD. It is worth noting that PRIME discovers the circadian rhythmic patterns without requiring the sample's timestamps. The codes for PRIME, along with codes to reproduce the figures in this paper, are available at https://github.com/xinxingwu-uk/PRIME.

On the algebraic structures of the space of interval-valued intuitionistic fuzzy numbers

This study is inspired by those of Huang et al. (Soft Comput. 25, 2513--2520, 2021) and Wang et al. (Inf. Sci. 179, 3026--3040, 2009) in which some ranking techniques for interval-valued intuitionistic fuzzy numbers (IVIFNs) were introduced. In this study, we prove that the space of all IVIFNs with the relation in the method for comparing any two IVIFNs based on a score function and three types of entropy functions is a complete chain and obtain that this relation is an admissible order. Moreover, we demonstrate that IVIFNs are complete chains to the relation in the comparison method for IVIFNs on the basis of score, accuracy, membership uncertainty index, and hesitation uncertainty index functions.

Topological and Algebraic Structures of the Space of Atanassov's Intuitionistic Fuzzy Values

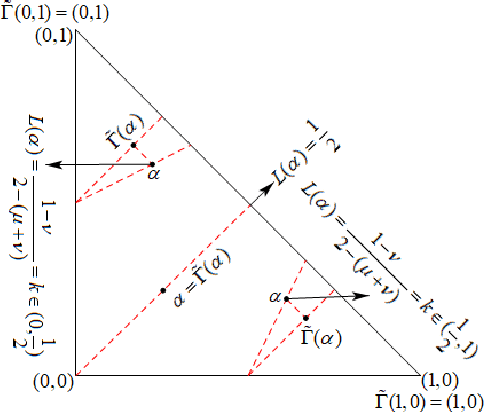
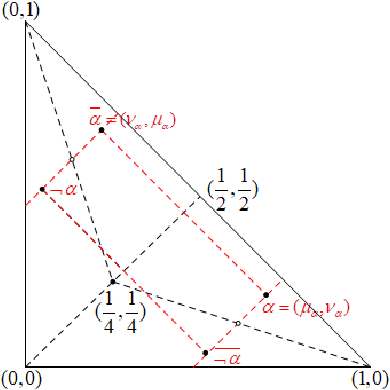
We demonstrate that the space of intuitionistic fuzzy values (IFVs) with the linear order based on a score function and an accuracy function has the same algebraic structure as the one induced by the linear order based on a similarity function and an accuracy function. By introducing a new operator for IFVs via the linear order based on a score function and an accuracy function, we present that such an operator is a strong negation on IFVs. Moreover, we propose that the space of IFVs is a complete lattice and a Kleene algebra with the new operator. We also observe that the topological space of IFVs with the order topology induced by the above two linear orders is not separable and metrizable but compact and connected. From exactly new perspectives, our results partially answer three open problems posed by Atanassov [Intuitionistic Fuzzy Sets: Theory and Applications, Springer, 1999] and [On Intuitionistic Fuzzy Sets Theory, Springer, 2012]. Furthermore, we construct an isomorphism between the spaces of IFVs and q-rung orthopedic fuzzy values (q-ROFVs) under the corresponding linear orders. Meanwhile, we introduce the concept of the admissible similarity measures with particular orders for IFSs, extending the previous definition of the similarity measure for IFSs, and construct an admissible similarity measure with the linear order based on a score function and an accuracy function, which is effectively applied to a pattern recognition problem about the classification of building materials.

Top-$k$ Regularization for Supervised Feature Selection

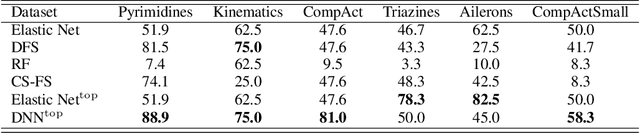
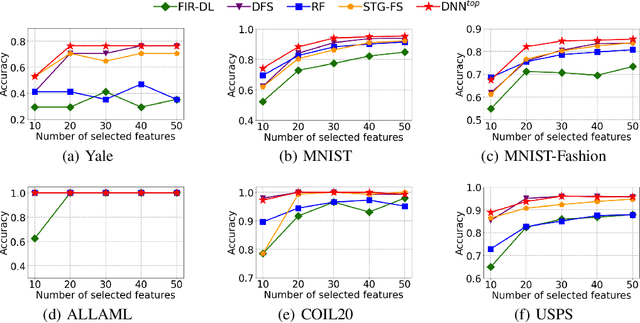
Feature selection identifies subsets of informative features and reduces dimensions in the original feature space, helping provide insights into data generation or a variety of domain problems. Existing methods mainly depend on feature scoring functions or sparse regularizations; nonetheless, they have limited ability to reconcile the representativeness and inter-correlations of features. In this paper, we introduce a novel, simple yet effective regularization approach, named top-$k$ regularization, to supervised feature selection in regression and classification tasks. Structurally, the top-$k$ regularization induces a sub-architecture on the architecture of a learning model to boost its ability to select the most informative features and model complex nonlinear relationships simultaneously. Theoretically, we derive and mathematically prove a uniform approximation error bound for using this approach to approximate high-dimensional sparse functions. Extensive experiments on a wide variety of benchmarking datasets show that the top-$k$ regularization is effective and stable for supervised feature selection.

Deepened Graph Auto-Encoders Help Stabilize and Enhance Link Prediction

Graph neural networks have been used for a variety of learning tasks, such as link prediction, node classification, and node clustering. Among them, link prediction is a relatively under-studied graph learning task, with current state-of-the-art models based on one- or two-layer of shallow graph auto-encoder (GAE) architectures. In this paper, we focus on addressing a limitation of current methods for link prediction, which can only use shallow GAEs and variational GAEs, and creating effective methods to deepen (variational) GAE architectures to achieve stable and competitive performance. Our proposed methods innovatively incorporate standard auto-encoders (AEs) into the architectures of GAEs, where standard AEs are leveraged to learn essential, low-dimensional representations via seamlessly integrating the adjacency information and node features, while GAEs further build multi-scaled low-dimensional representations via residual connections to learn a compact overall embedding for link prediction. Empirically, extensive experiments on various benchmarking datasets verify the effectiveness of our methods and demonstrate the competitive performance of our deepened graph models for link prediction. Theoretically, we prove that our deep extensions inclusively express multiple polynomial filters with different orders.

Fractal Autoencoders for Feature Selection

Feature selection reduces the dimensionality of data by identifying a subset of the most informative features. In this paper, we propose an innovative framework for unsupervised feature selection, called fractal autoencoders (FAE). It trains a neural network (NN) to pinpoint informative features for global exploring of representability and for local excavating of diversity. Architecturally, FAE extends autoencoders by adding a one-to-one scoring layer and a small sub-NN for feature selection in an unsupervised fashion. With such a concise architecture, FAE achieves state-of-the-art performances; extensive experimental results on fourteen datasets, including very high-dimensional data, have demonstrated the superiority of FAE over existing contemporary methods for unsupervised feature selection. In particular, FAE exhibits substantial advantages on gene expression data exploration, reducing measurement cost by about 15% over the widely used L1000 landmark genes. Further, we show that the FAE framework is easily extensible with an application.

A Uniformly Stable Algorithm For Unsupervised Feature Selection

High-dimensional data presents challenges for data management. Feature selection, as an important dimensionality reduction technique, reduces the dimensionality of data by identifying an essential subset of input features, and it can provide interpretable, effective, and efficient insights for analysis and decision-making processes. Algorithmic stability is a key characteristic of an algorithm in its sensitivity to perturbations of input samples. In this paper, first we propose an innovative unsupervised feature selection algorithm. The architecture of our algorithm consists of a feature scorer and a feature selector. The scorer trains a neural network (NN) to score all the features globally, and the selector is in a dependence sub-NN which locally evaluates the representation abilities to select features. Further, we present algorithmic stability analysis and show our algorithm has a performance guarantee by providing a generalization error bound. Empirically, extensive experimental results on ten real-world datasets corroborate the superior generalization performance of our algorithm over contemporary algorithms. Notably, the features selected by our algorithm have comparable performance to the original features; therefore, our algorithm significantly facilitates data management.

Distribution-dependent concentration inequalities for tighter generalization bounds

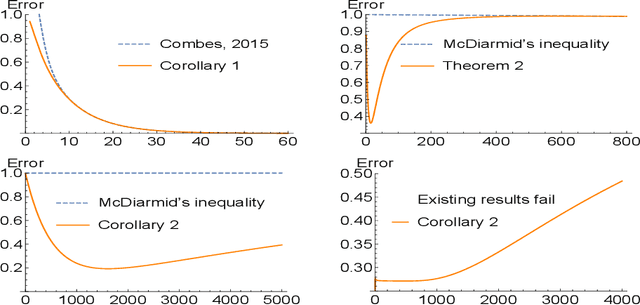
Concentration inequalities are indispensable tools for studying the generalization capacity of learning models. Hoeffding's and McDiarmid's inequalities are commonly used, giving bounds independent of the data distribution. Although this makes them widely applicable, a drawback is that the bounds can be too loose in some specific cases. Although efforts have been devoted to improving the bounds, we find that the bounds can be further tightened in some distribution-dependent scenarios and conditions for the inequalities can be relaxed. In particular, we propose four types of conditions for probabilistic boundedness and bounded differences, and derive several distribution-dependent extensions of Hoeffding's and McDiarmid's inequalities. These extensions provide bounds for functions not satisfying the conditions of the existing inequalities, and in some special cases, tighter bounds. Furthermore, we obtain generalization bounds for unbounded and hierarchy-bounded loss functions. Finally we discuss the potential applications of our extensions to learning theory.