Distribution-dependent concentration inequalities for tighter generalization bounds
Paper and Code
Feb 20, 2017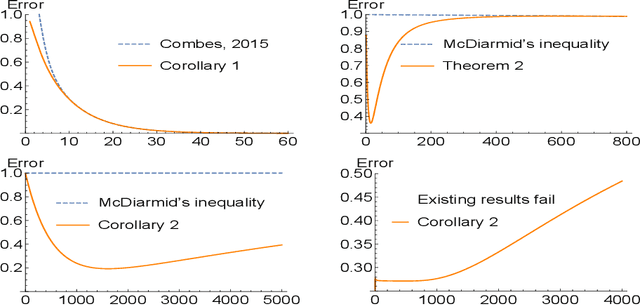
Concentration inequalities are indispensable tools for studying the generalization capacity of learning models. Hoeffding's and McDiarmid's inequalities are commonly used, giving bounds independent of the data distribution. Although this makes them widely applicable, a drawback is that the bounds can be too loose in some specific cases. Although efforts have been devoted to improving the bounds, we find that the bounds can be further tightened in some distribution-dependent scenarios and conditions for the inequalities can be relaxed. In particular, we propose four types of conditions for probabilistic boundedness and bounded differences, and derive several distribution-dependent extensions of Hoeffding's and McDiarmid's inequalities. These extensions provide bounds for functions not satisfying the conditions of the existing inequalities, and in some special cases, tighter bounds. Furthermore, we obtain generalization bounds for unbounded and hierarchy-bounded loss functions. Finally we discuss the potential applications of our extensions to learning theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge