Top-$k$ Regularization for Supervised Feature Selection
Paper and Code
Jun 04, 2021

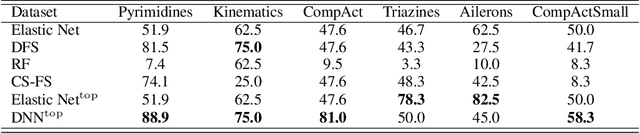
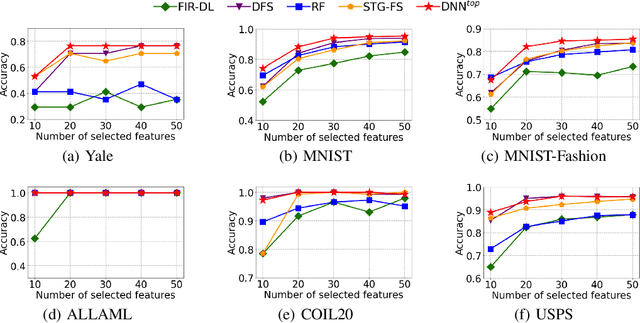
Feature selection identifies subsets of informative features and reduces dimensions in the original feature space, helping provide insights into data generation or a variety of domain problems. Existing methods mainly depend on feature scoring functions or sparse regularizations; nonetheless, they have limited ability to reconcile the representativeness and inter-correlations of features. In this paper, we introduce a novel, simple yet effective regularization approach, named top-$k$ regularization, to supervised feature selection in regression and classification tasks. Structurally, the top-$k$ regularization induces a sub-architecture on the architecture of a learning model to boost its ability to select the most informative features and model complex nonlinear relationships simultaneously. Theoretically, we derive and mathematically prove a uniform approximation error bound for using this approach to approximate high-dimensional sparse functions. Extensive experiments on a wide variety of benchmarking datasets show that the top-$k$ regularization is effective and stable for supervised feature selection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge