Topological and Algebraic Structures of the Space of Atanassov's Intuitionistic Fuzzy Values
Paper and Code
Nov 17, 2021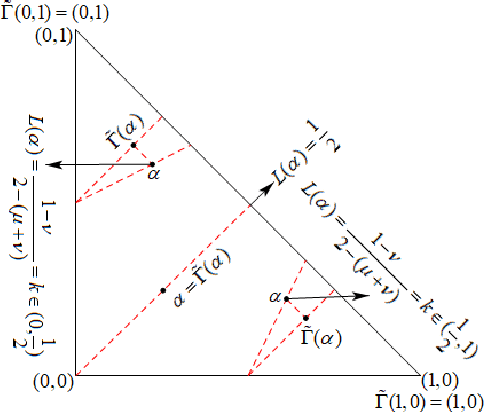
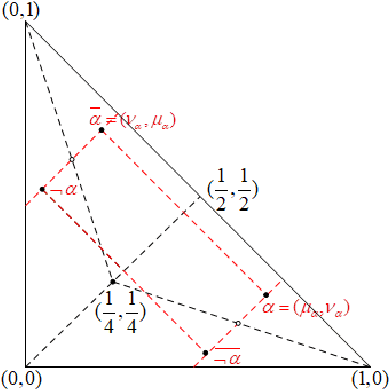
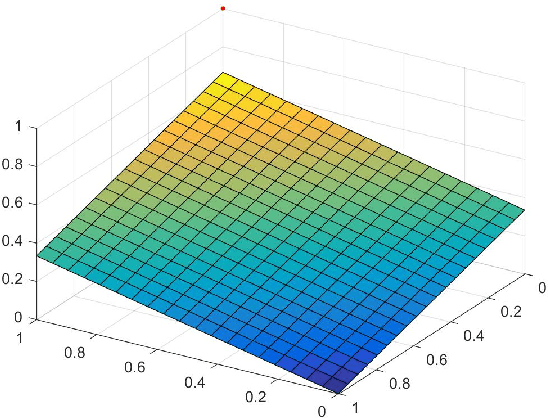
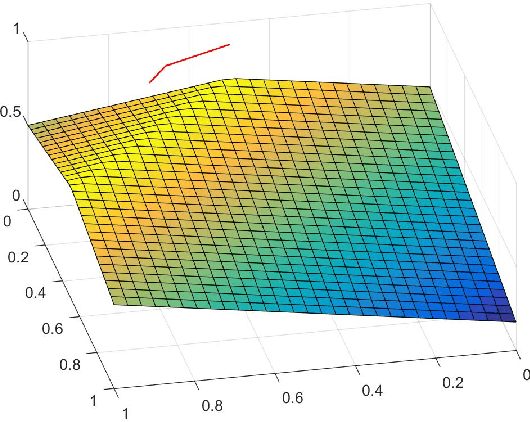
We demonstrate that the space of intuitionistic fuzzy values (IFVs) with the linear order based on a score function and an accuracy function has the same algebraic structure as the one induced by the linear order based on a similarity function and an accuracy function. By introducing a new operator for IFVs via the linear order based on a score function and an accuracy function, we present that such an operator is a strong negation on IFVs. Moreover, we propose that the space of IFVs is a complete lattice and a Kleene algebra with the new operator. We also observe that the topological space of IFVs with the order topology induced by the above two linear orders is not separable and metrizable but compact and connected. From exactly new perspectives, our results partially answer three open problems posed by Atanassov [Intuitionistic Fuzzy Sets: Theory and Applications, Springer, 1999] and [On Intuitionistic Fuzzy Sets Theory, Springer, 2012]. Furthermore, we construct an isomorphism between the spaces of IFVs and q-rung orthopedic fuzzy values (q-ROFVs) under the corresponding linear orders. Meanwhile, we introduce the concept of the admissible similarity measures with particular orders for IFSs, extending the previous definition of the similarity measure for IFSs, and construct an admissible similarity measure with the linear order based on a score function and an accuracy function, which is effectively applied to a pattern recognition problem about the classification of building materials.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge