Deep-learning-aided Low-complexity DOA Estimators for Ultra-Massive MIMO Overlapped Receive Array

Massive multiple input multiple output(MIMO)-based fully-digital receive antenna arrays bring huge amount of complexity to both traditional direction of arrival(DOA) estimation algorithms and neural network training, which is difficult to satisfy high-precision and low-latency applications in future wireless communications. To address this challenge, two estimators called OPSC and OSAP-CBAM-CNN are proposed in this paper. The computational complexity of the traditional DOA algorithm is first considered to be reduced by dividing the total set of antennas into multiple overlapped subarrays uniformly, each subarray crosses each other proportionally and performs DOA estimation to generate coarse angles, and all angles are coherently combined to get the better estimation, the final DOA estimation can given by maximum likelihood alternating projection(ML-AP) in a very small range, which has a better performance than the direct partitioning of subarrays. To further reduce the complexity of traditional estimation algorithms, deep neural networks(DNN) are utilized to offline train the relationship between the received signal covariance matrix and the estimated angles. Due to the high complexity of the training network based on large-scale arrays, in the OSAP-CBAM-CNN method, the complex network is divided into several smaller networks based on the overlapped subarray to give rough DOA estimations, followed by coherent combining and AP algorithm to get the final DOA estimation. Simulation results show that as the number of antennas goes to large-scale, the proposed methods can achieve a remarkable complexity reduction over conventional ML-AP algorithm.

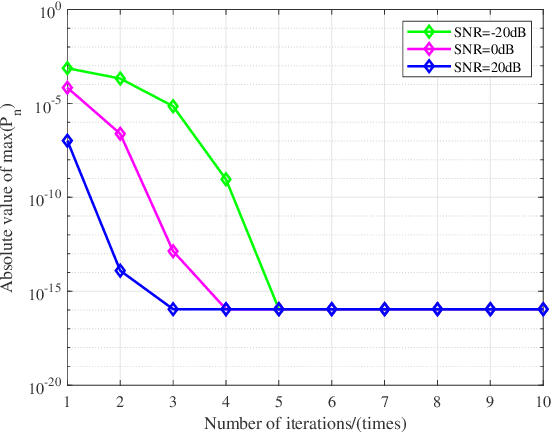
A Rapid Power-iterative Root-MUSIC Estimator for Massive/Ultra-massive MIMO Receiver

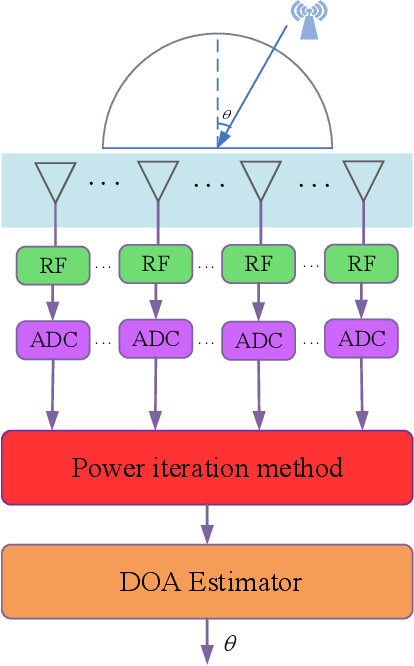
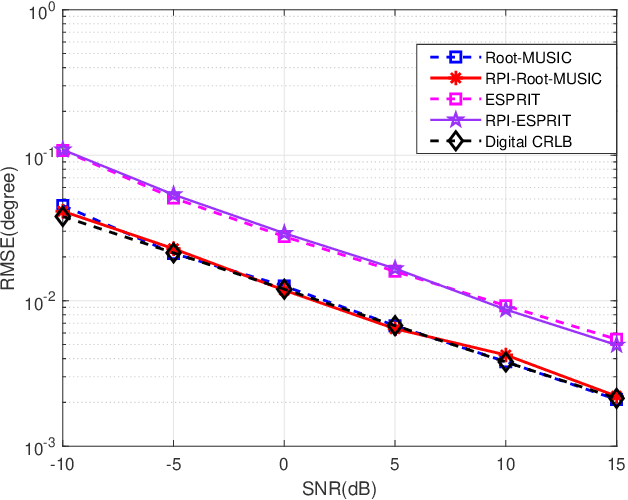
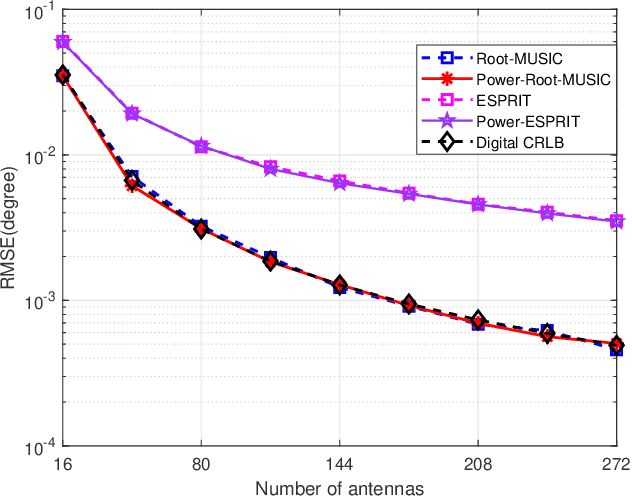
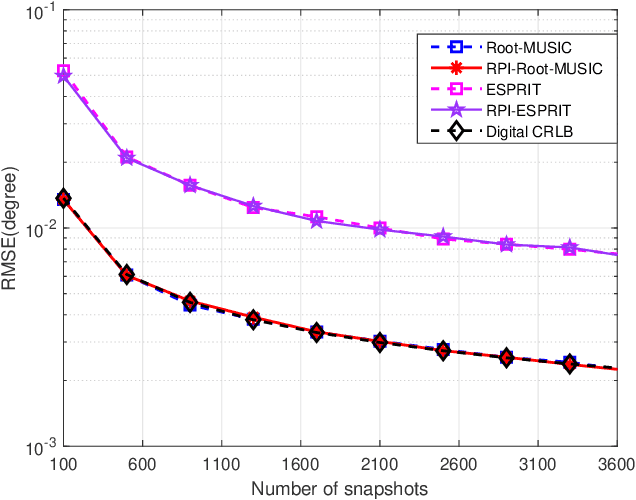
For a passive direction of arrival (DOA) measurement system using massive multiple input multiple output (MIMO), the complexity of the covariance matrix decompositionbased DOA measurement method is extremely high. To significantly reduce the computational complexity, two strategies are proposed. Firstly, a rapid power-iterative estimation of signal parameters via rotational invariance technique (RPI-ESPRIT) method is proposed, which not only reduces the complexity but also achieves good directional measurement results. However, the general complexity is still high. In order to further the complexity, a rapid power-iterative root Multiple Signal Classification (RPIRoot-MUSIC) method is proposed. Simulation results show that the two proposed methods outperform the classical DOA estimation method in terms of computational complexity. In particular, the lowest complexity achieved by the RPI-Root-MUSIC method is about two-order-magnitude lower than that of Root-MUSIC in terms of FLOP. In addition, it is verified that the initial vector and relative error have a substantial effect on the performance of computational complexity.

Rapid Phase Ambiguity Elimination Methods for DOA Estimator via Hybrid Massive MIMO Receive Array

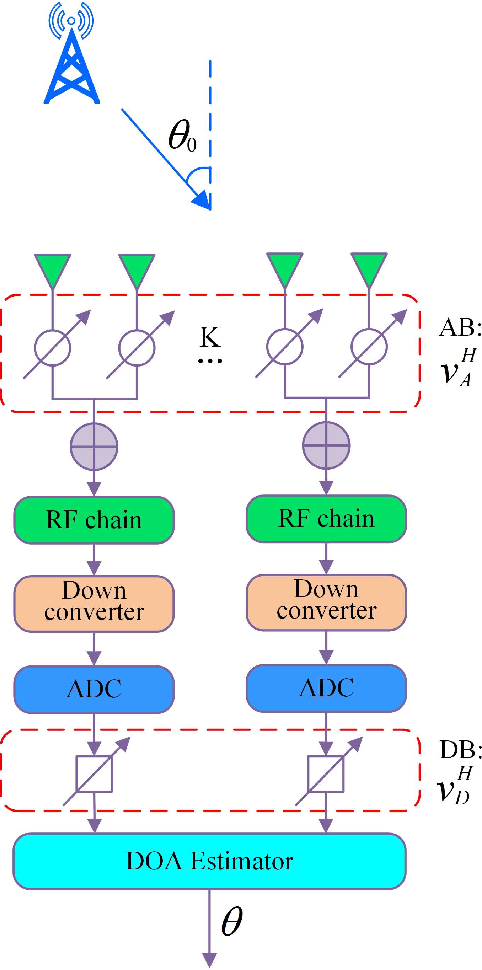
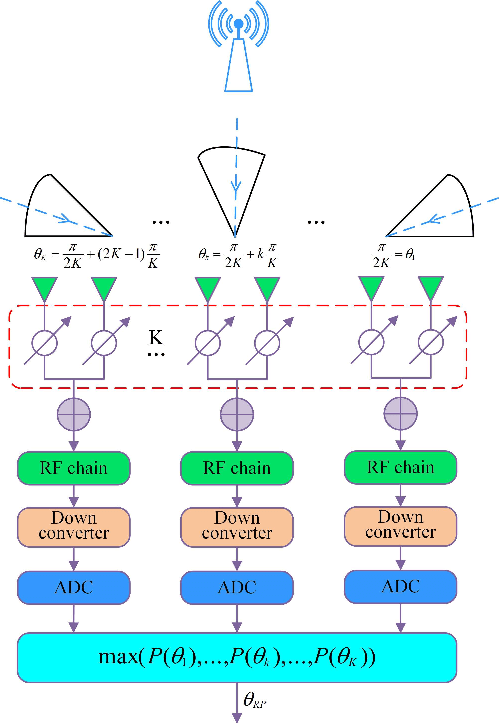
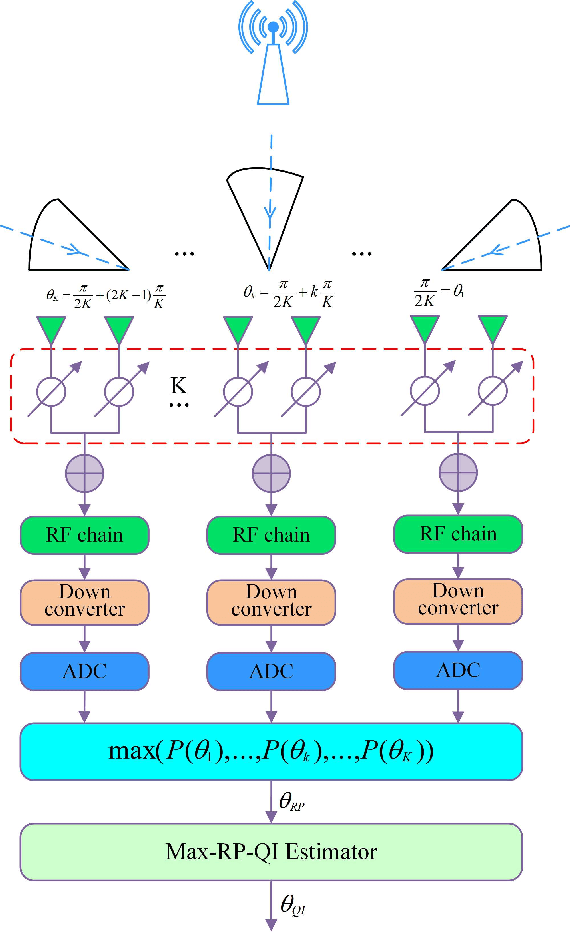
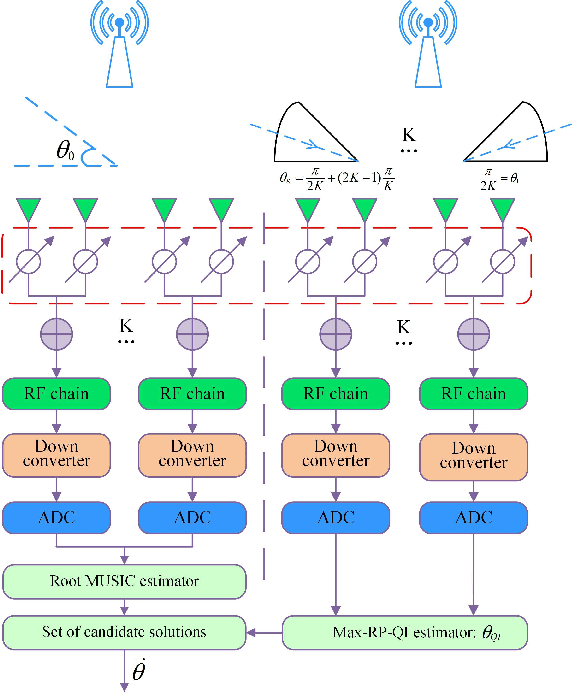
For a sub-connected hybrid multiple-input multiple-output (MIMO) receiver with $K$ subarrays and $N$ antennas, there exists a challenging problem of how to rapidly remove phase ambiguity in only single time-slot. First, a DOA estimator of maximizing received power (Max-RP) is proposed to find the maximum value of $K$-subarray output powers, where each subarray is in charge of one sector, and the center angle of the sector corresponding to the maximum output is the estimated true DOA. To make an enhancement on precision, Max-RP plus quadratic interpolation (Max-RP-QI) method is designed. In the proposed Max-RP-QI, a quadratic interpolation scheme is adopted to interpolate the three DOA values corresponding to the largest three receive powers of Max-RP. Finally, to achieve the CRLB, a Root-MUSIC plus Max-RP-QI scheme is developed. Simulation results show that the proposed three methods eliminate the phase ambiguity during one time-slot and also show low-computational-complexities. In particular, the proposed Root-MUSIC plus Max-RP-QI scheme can reach the CRLB, and the proposed Max-RP and Max-RP-QI are still some performance losses $2dB\thicksim4dB$ compared to the CRLB.

Two Low-complexity DOA Estimators for Massive/Ultra-massive MIMO Receive Array

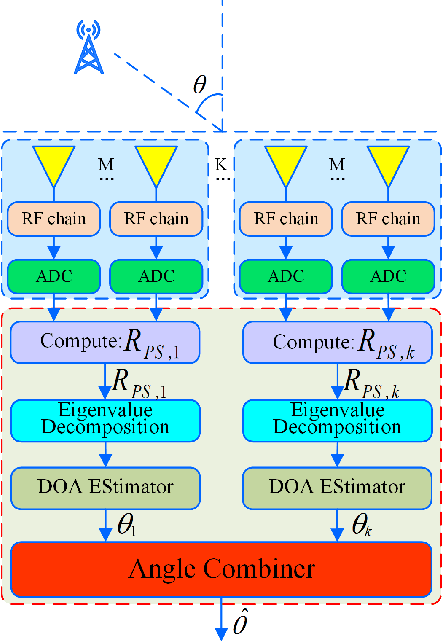
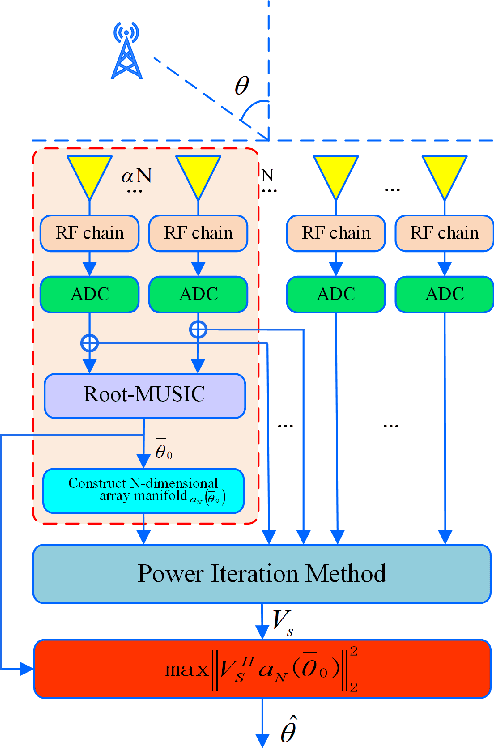
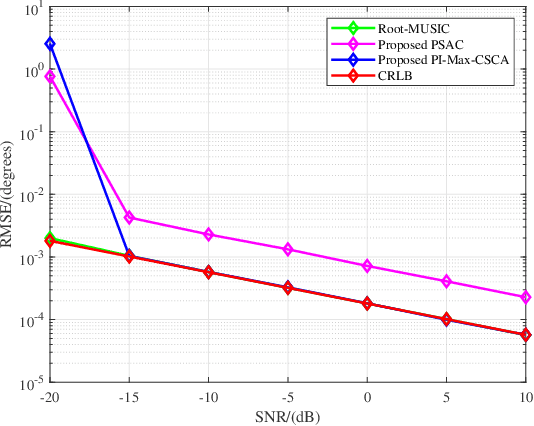
Eigen-decomposition-based direction finding methods of using large-scale/ultra-large-scale fully-digital receive antenna arrays leads to a high or ultra-high complexity. To address the complexity dilemma, in this paper, two low-complexity estimators are proposed: partitioned subarray combining (PSAC) and power iteration max correlation successive convex approximation (PI-Max-CSCA). Compared with the conventional no-partitioned direction finding method like root multiple signal classification (Root-MUSIC), in PSAC method, the total set of antennas are equally partitioned into subsets of antennas, called subarrays, each subarray performs independent DOA estimation, and finally all DOA estimates are coherently combined to give the final estimate. In PI-Max-CSCA method, using a fraction of all subarrays to make an initial coarse direction measurement (ICDM), the power iterative method is adopted to compute the more precise steering vector (SV) by exploiting the total array, and a more accurate DOA value is found using ICDM and SV through the maximum correlation method solved by successive convex approximation.

Machine-learning-aided Massive Hybrid Analog and Digital MIMO DOA Estimation for Future Wireless Networks

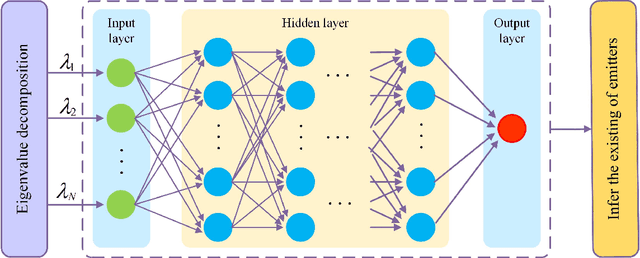
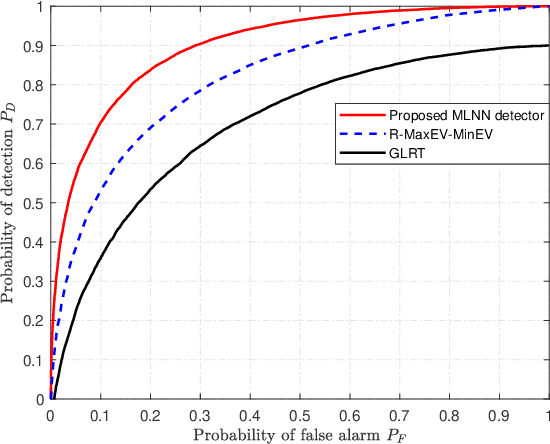
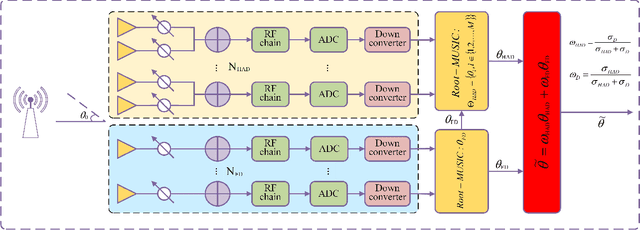
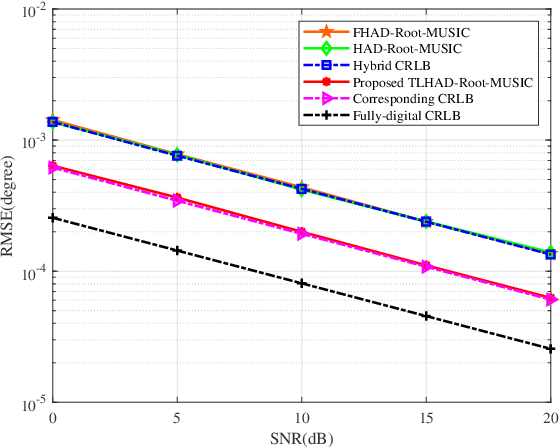
Due to a high spatial angle resolution and low circuit cost of massive hybrid analog and digital (HAD) multiple-input multiple-output (MIMO), it is viewed as a key technology for future wireless networks. Combining a massive HAD-MIMO with direction of arrinal (DOA) will provide a high-precision even ultra-high-precision DOA measurement performance approaching the fully-digital (FD) MIMO. However, phase ambiguity is a challenge issue for a massive HAD-MIMO DOA estimation. In this paper, we review three aspects: detection, estimation, and Cramer-Rao lower bound (CRLB) with low-resolution ADCs at receiver. First, a multi-layer-neural-network (MLNN) detector is proposed to infer the existence of passive emitters. Then, a two-layer HAD (TLHAD) MIMO structure is proposed to eliminate phase ambiguity using only one-snapshot. Simulation results show that the proposed MLNN detector is much better than both the existing generalized likelihood ratio test (GRLT) and the ratio of maximum eigen-value (Max-EV) to minimum eigen-value (R-MaxEV-MinEV) in terms of detection probability. Additionally, the proposed TLHAD structure can achieve the corresponding CRLB using single snapshot.

High-performance Passive Eigen-model-based Detectors of Single Emitter Using Massive MIMO Receivers

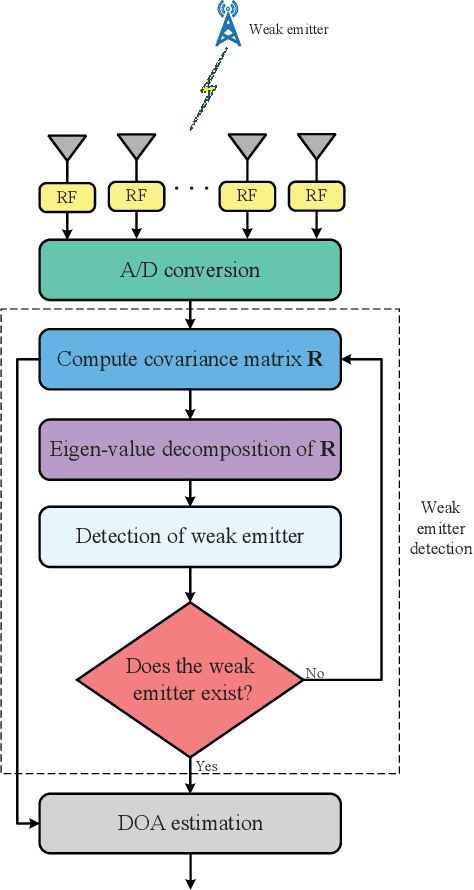
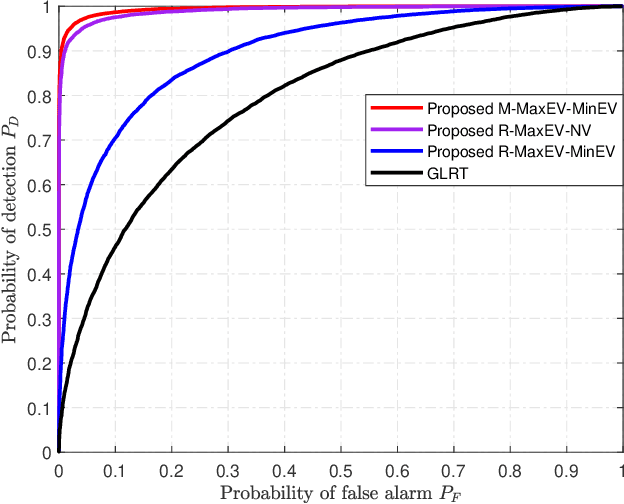
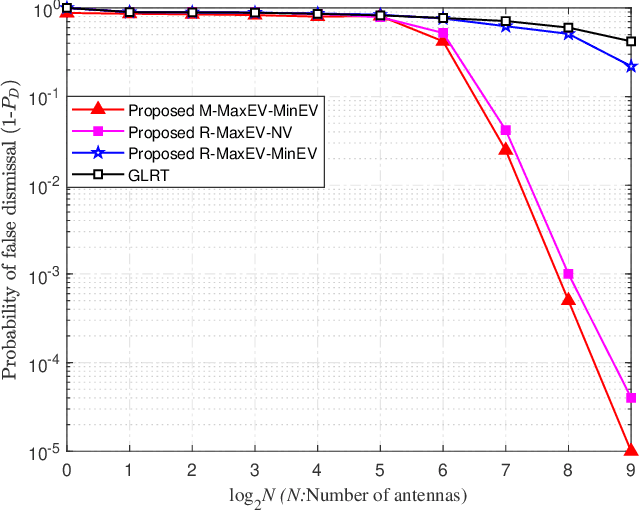
For a passive direction of arrival (DoA) measurement system using massive multiple input multiple output (MIMO), it is mandatory to infer whether the emitter exists or not before performing DOA estimation operation. Inspired by the detection idea from radio detection and ranging (radar), three high-performance detectors are proposed to infer the existence of single passive emitter from the eigen-space of sample covariance matrix of receive signal vector. The test statistic (TS) of the first method is defined as the ratio of maximum eigen-value (Max-EV) to minimum eigen-value (R-MaxEV-MinEV) while that of the second one is defined as the ratio of Max-EV to noise variance (R-MaxEV-NV). The TS of the third method is the mean of maximum eigen-value (EV) and minimum EV(M-MaxEV-MinEV). Their closed-form expressions are presented and the corresponding detection performance is given. Simulation results show that the proposed M-MaxEV-MinEV and R-MaxEV-NV methods can approximately achieve the same detection performance that is better than the traditional generalized likelihood ratio test method with false alarm probability being less than 0.3.