Rapid Phase Ambiguity Elimination Methods for DOA Estimator via Hybrid Massive MIMO Receive Array

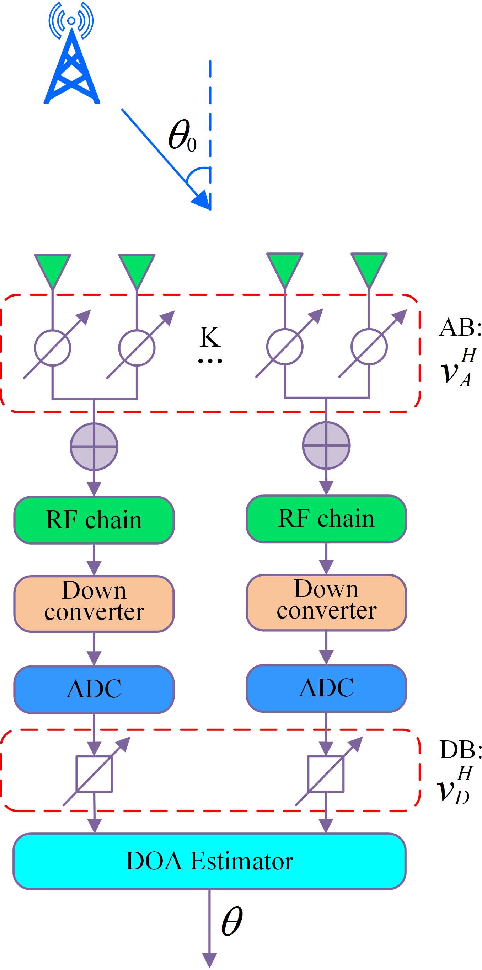
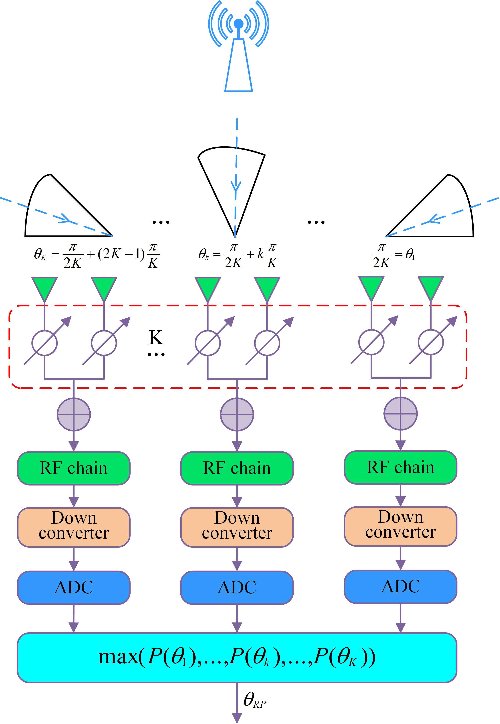
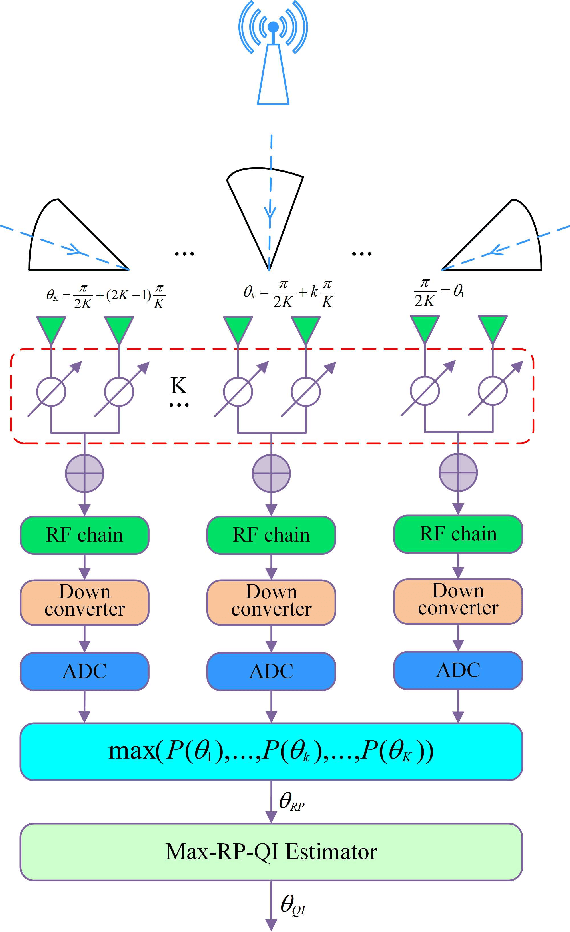
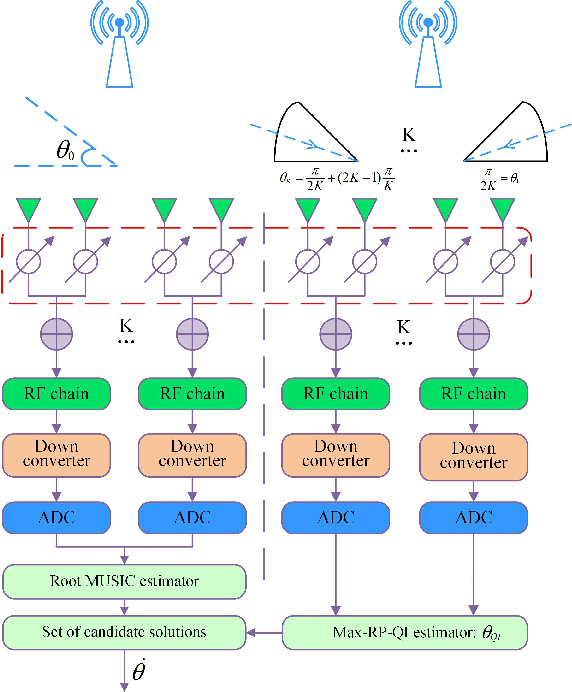
For a sub-connected hybrid multiple-input multiple-output (MIMO) receiver with $K$ subarrays and $N$ antennas, there exists a challenging problem of how to rapidly remove phase ambiguity in only single time-slot. First, a DOA estimator of maximizing received power (Max-RP) is proposed to find the maximum value of $K$-subarray output powers, where each subarray is in charge of one sector, and the center angle of the sector corresponding to the maximum output is the estimated true DOA. To make an enhancement on precision, Max-RP plus quadratic interpolation (Max-RP-QI) method is designed. In the proposed Max-RP-QI, a quadratic interpolation scheme is adopted to interpolate the three DOA values corresponding to the largest three receive powers of Max-RP. Finally, to achieve the CRLB, a Root-MUSIC plus Max-RP-QI scheme is developed. Simulation results show that the proposed three methods eliminate the phase ambiguity during one time-slot and also show low-computational-complexities. In particular, the proposed Root-MUSIC plus Max-RP-QI scheme can reach the CRLB, and the proposed Max-RP and Max-RP-QI are still some performance losses $2dB\thicksim4dB$ compared to the CRLB.

Machine-learning-aided Massive Hybrid Analog and Digital MIMO DOA Estimation for Future Wireless Networks

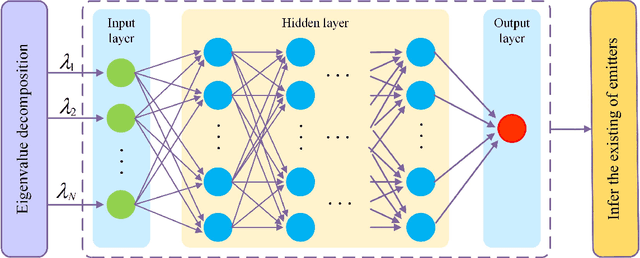
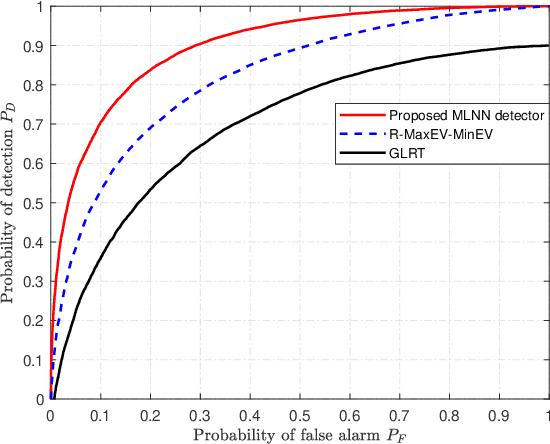
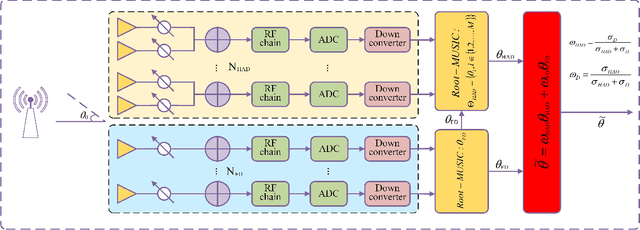
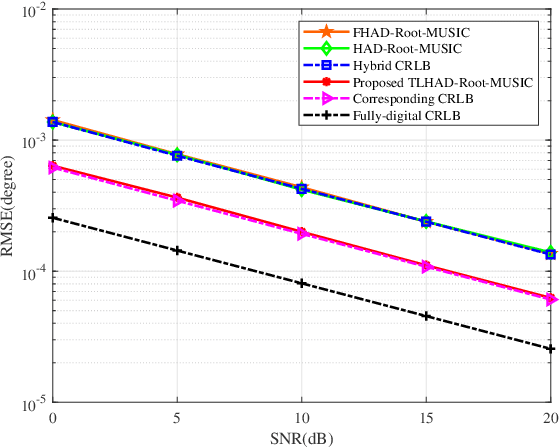
Due to a high spatial angle resolution and low circuit cost of massive hybrid analog and digital (HAD) multiple-input multiple-output (MIMO), it is viewed as a key technology for future wireless networks. Combining a massive HAD-MIMO with direction of arrinal (DOA) will provide a high-precision even ultra-high-precision DOA measurement performance approaching the fully-digital (FD) MIMO. However, phase ambiguity is a challenge issue for a massive HAD-MIMO DOA estimation. In this paper, we review three aspects: detection, estimation, and Cramer-Rao lower bound (CRLB) with low-resolution ADCs at receiver. First, a multi-layer-neural-network (MLNN) detector is proposed to infer the existence of passive emitters. Then, a two-layer HAD (TLHAD) MIMO structure is proposed to eliminate phase ambiguity using only one-snapshot. Simulation results show that the proposed MLNN detector is much better than both the existing generalized likelihood ratio test (GRLT) and the ratio of maximum eigen-value (Max-EV) to minimum eigen-value (R-MaxEV-MinEV) in terms of detection probability. Additionally, the proposed TLHAD structure can achieve the corresponding CRLB using single snapshot.