Reasoning and Sampling-Augmented MCQ Difficulty Prediction via LLMs

The difficulty of multiple-choice questions (MCQs) is a crucial factor for educational assessments. Predicting MCQ difficulty is challenging since it requires understanding both the complexity of reaching the correct option and the plausibility of distractors, i.e., incorrect options. In this paper, we propose a novel, two-stage method to predict the difficulty of MCQs. First, to better estimate the complexity of each MCQ, we use large language models (LLMs) to augment the reasoning steps required to reach each option. We use not just the MCQ itself but also these reasoning steps as input to predict the difficulty. Second, to capture the plausibility of distractors, we sample knowledge levels from a distribution to account for variation among students responding to the MCQ. This setup, inspired by item response theory (IRT), enable us to estimate the likelihood of students selecting each (both correct and incorrect) option. We align these predictions with their ground truth values, using a Kullback-Leibler (KL) divergence-based regularization objective, and use estimated likelihoods to predict MCQ difficulty. We evaluate our method on two real-world \emph{math} MCQ and response datasets with ground truth difficulty values estimated using IRT. Experimental results show that our method outperforms all baselines, up to a 28.3\% reduction in mean squared error and a 34.6\% improvement in the coefficient of determination. We also qualitatively discuss how our novel method results in higher accuracy in predicting MCQ difficulty.

From Text to Visuals: Using LLMs to Generate Math Diagrams with Vector Graphics

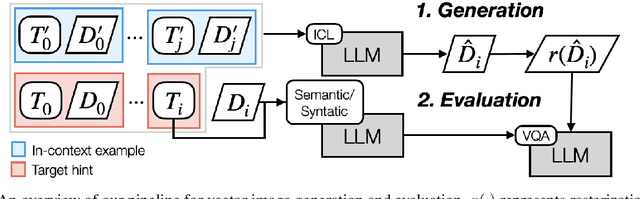
Advances in large language models (LLMs) offer new possibilities for enhancing math education by automating support for both teachers and students. While prior work has focused on generating math problems and high-quality distractors, the role of visualization in math learning remains under-explored. Diagrams are essential for mathematical thinking and problem-solving, yet manually creating them is time-consuming and requires domain-specific expertise, limiting scalability. Recent research on using LLMs to generate Scalable Vector Graphics (SVG) presents a promising approach to automating diagram creation. Unlike pixel-based images, SVGs represent geometric figures using XML, allowing seamless scaling and adaptability. Educational platforms such as Khan Academy and IXL already use SVGs to display math problems and hints. In this paper, we explore the use of LLMs to generate math-related diagrams that accompany textual hints via intermediate SVG representations. We address three research questions: (1) how to automatically generate math diagrams in problem-solving hints and evaluate their quality, (2) whether SVG is an effective intermediate representation for math diagrams, and (3) what prompting strategies and formats are required for LLMs to generate accurate SVG-based diagrams. Our contributions include defining the task of automatically generating SVG-based diagrams for math hints, developing an LLM prompting-based pipeline, and identifying key strategies for improving diagram generation. Additionally, we introduce a Visual Question Answering-based evaluation setup and conduct ablation studies to assess different pipeline variations. By automating the math diagram creation, we aim to provide students and teachers with accurate, conceptually relevant visual aids that enhance problem-solving and learning experiences.

Exploring Automated Distractor Generation for Math Multiple-choice Questions via Large Language Models

Multiple-choice questions (MCQs) are ubiquitous in almost all levels of education since they are easy to administer, grade, and are a reliable format in assessments and practices. One of the most important aspects of MCQs is the distractors, i.e., incorrect options that are designed to target common errors or misconceptions among real students. To date, the task of crafting high-quality distractors largely remains a labor and time-intensive process for teachers and learning content designers, which has limited scalability. In this work, we study the task of automated distractor generation in the domain of math MCQs and explore a wide variety of large language model (LLM)-based approaches, from in-context learning to fine-tuning. We conduct extensive experiments using a real-world math MCQ dataset and find that although LLMs can generate some mathematically valid distractors, they are less adept at anticipating common errors or misconceptions among real students.

Exploring Automated Distractor and Feedback Generation for Math Multiple-choice Questions via In-context Learning

Multiple-choice questions (MCQs) are ubiquitous in almost all levels of education since they are easy to administer, grade, and are a reliable format in both assessments and practices. An important aspect of MCQs is the distractors, i.e., incorrect options that are designed to target specific misconceptions or insufficient knowledge among students. To date, the task of crafting high-quality distractors has largely remained a labor-intensive process for teachers and learning content designers, which has limited scalability. In this work, we explore the task of automated distractor and corresponding feedback message generation in math MCQs using large language models. We establish a formulation of these two tasks and propose a simple, in-context learning-based solution. Moreover, we explore using two non-standard metrics to evaluate the quality of the generated distractors and feedback messages. We conduct extensive experiments on these tasks using a real-world MCQ dataset that contains student response information. Our findings suggest that there is a lot of room for improvement in automated distractor and feedback generation. We also outline several directions for future work

A Conceptual Model for End-to-End Causal Discovery in Knowledge Tracing

In this paper, we take a preliminary step towards solving the problem of causal discovery in knowledge tracing, i.e., finding the underlying causal relationship among different skills from real-world student response data. This problem is important since it can potentially help us understand the causal relationship between different skills without extensive A/B testing, which can potentially help educators to design better curricula according to skill prerequisite information. Specifically, we propose a conceptual solution, a novel causal gated recurrent unit (GRU) module in a modified deep knowledge tracing model, which uses i) a learnable permutation matrix for causal ordering among skills and ii) an optionally learnable lower-triangular matrix for causal structure among skills. We also detail how to learn the model parameters in an end-to-end, differentiable way. Our solution placed among the top entries in Task 3 of the NeurIPS 2022 Challenge on Causal Insights for Learning Paths in Education. We detail preliminary experiments as evaluated on the challenge's public leaderboard since the ground truth causal structure has not been publicly released, making detailed local evaluation impossible.