Inference on weighted average value function in high-dimensional state space

This paper gives a consistent, asymptotically normal estimator of the expected value function when the state space is high-dimensional and the first-stage nuisance functions are estimated by modern machine learning tools. First, we show that value function is orthogonal to the conditional choice probability, therefore, this nuisance function needs to be estimated only at $n^{-1/4}$ rate. Second, we give a correction term for the transition density of the state variable. The resulting orthogonal moment is robust to misspecification of the transition density and does not require this nuisance function to be consistently estimated. Third, we generalize this result by considering the weighted expected value. In this case, the orthogonal moment is doubly robust in the transition density and additional second-stage nuisance functions entering the correction term. We complete the asymptotic theory by providing bounds on second-order asymptotic terms.

Machine Learning for Set-Identified Linear Models

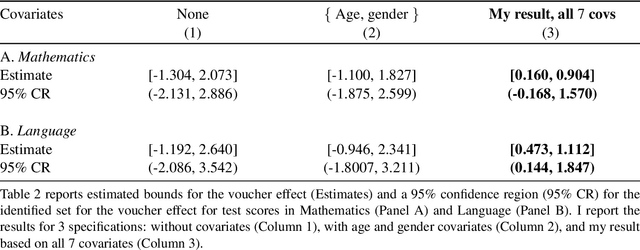
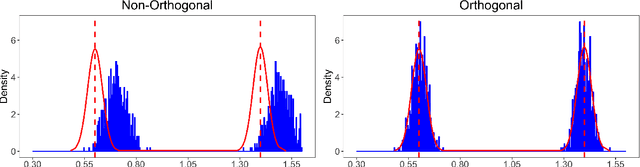
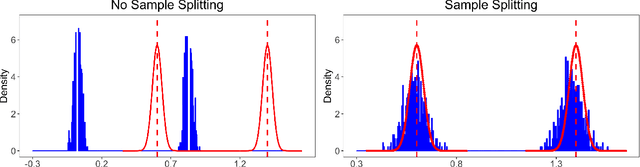
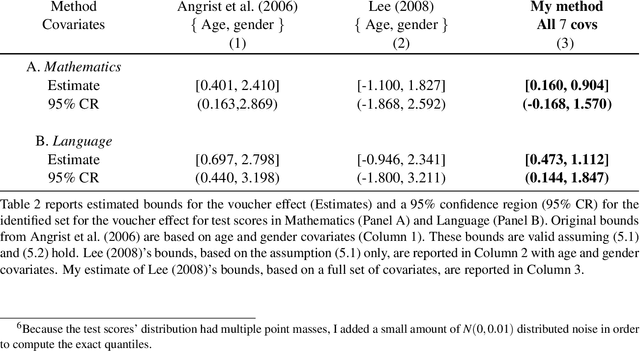
Set-identified models often restrict the number of covariates leading to wide identified sets in practice. This paper provides estimation and inference methods for set-identified linear models with high-dimensional covariates where the model selection is based on modern machine learning tools. I characterize the boundary (i.e, support function) of the identified set using a semiparametric moment condition. Combining Neyman-orthogonality and sample splitting ideas, I construct a root-N consistent, the uniformly asymptotically Gaussian estimator of the support function. I also prove the validity of the Bayesian bootstrap procedure to conduct inference about the identified set. I provide a general method to construct a Neyman-orthogonal moment condition for the support function. I apply this result to estimate sharp nonparametric bounds on the average treatment effect in Lee (2008)'s model of endogenous selection and substantially tighten the bounds on this parameter in Angrist et al. (2006)'s empirical setting. I also apply this result to estimate sharp identified sets for two other parameters - a new parameter, called a partially linear predictor, and the average partial derivative when the outcome variable is recorded in intervals.

Plug-in Regularized Estimation of High-Dimensional Parameters in Nonlinear Semiparametric Models

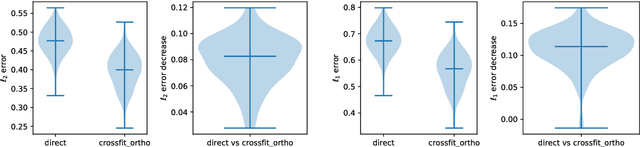
We develop a theory for estimation of a high-dimensional sparse parameter $\theta$ defined as a minimizer of a population loss function $L_D(\theta,g_0)$ which, in addition to $\theta$, depends on a, potentially infinite dimensional, nuisance parameter $g_0$. Our approach is based on estimating $\theta$ via an $\ell_1$-regularized minimization of a sample analog of $L_S(\theta, \hat{g})$, plugging in a first-stage estimate $\hat{g}$, computed on a hold-out sample. We define a population loss to be (Neyman) orthogonal if the gradient of the loss with respect to $\theta$, has pathwise derivative with respect to $g$ equal to zero, when evaluated at the true parameter and nuisance component. We show that orthogonality implies a second-order impact of the first stage nuisance error on the second stage target parameter estimate. Our approach applies to both convex and non-convex losses, albeit the latter case requires a small adaptation of our method with a preliminary estimation step of the target parameter. Our result enables oracle convergence rates for $\theta$ under assumptions on the first stage rates, typically of the order of $n^{-1/4}$. We show how such an orthogonal loss can be constructed via a novel orthogonalization process for a general model defined by conditional moment restrictions. We apply our theory to high-dimensional versions of standard estimation problems in statistics and econometrics, such as: estimation of conditional moment models with missing data, estimation of structural utilities in games of incomplete information and estimation of treatment effects in regression models with non-linear link functions.

Simultaneous Inference for Best Linear Predictor of the Conditional Average Treatment Effect and Other Structural Functions

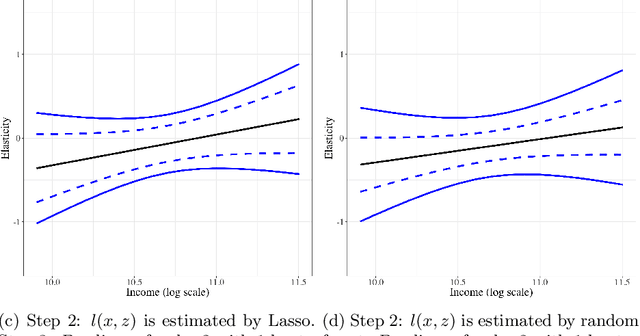
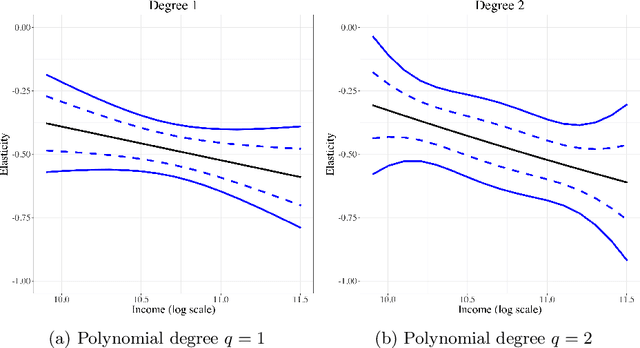
This paper provides estimation and inference methods for a structural function, such as Conditional Average Treatment Effect (CATE), based on modern machine learning (ML) tools. We assume that such function can be represented as an expectation g(x) of a signal Y conditional on X that depends on an unknown nuisance function. In addition to CATE, examples of such functions include regression function with Partially Missing Outcome and Conditional Average Partial Derivative. We approximate g(x) by a linear form that is a product of a vector of the approximating basis functions p(x) and the Best Linear Predictor (BLP), which we refer to a pseudo-target. Plugging in the first-stage estimate of the nuisance function into the signal, we estimate BLP via ordinary least squares. We deliver a high-quality estimate of the pseudo-target function that features (a) a pointwise Gaussian approximation, (b) a simultaneous Gaussian approximation, and (c) optimal rate of simultaneous convergence. In the case, the misspecification error of the linear form decays sufficiently fast, these approximations automatically hold for the target function g(x) instead of a pseudo-target. The first stage nuisance parameter is allowed to be high-dimensional and is estimated by modern ML tools, such as neural networks, shrinkage estimators, and random forest. Using our method, we estimate the average price elasticity conditional on income using Yatchew and No (2001) data and provide simultaneous confidence bands for the target regression function.

Orthogonal Machine Learning for Demand Estimation: High Dimensional Causal Inference in Dynamic Panels

There has been growing interest in how economists can import machine learning tools designed for prediction to accelerate and automate the model selection process, while still retaining desirable inference properties for causal parameters. Focusing on partially linear models, we extend the Double ML framework to allow for (1) a number of treatments that may grow with the sample size and (2) the analysis of panel data under sequentially exogenous errors. Our low-dimensional treatment (LD) regime directly extends the work in [Chernozhukov et al., 2016], by showing that the coefficients from a second stage, ordinary least squares estimator attain root-n convergence and desired coverage even if the dimensionality of treatment is allowed to grow. In a high-dimensional sparse (HDS) regime, we show that second stage LASSO and debiased LASSO have asymptotic properties equivalent to oracle estimators with no upstream error. We argue that these advances make Double ML methods a desirable alternative for practitioners estimating short-term demand elasticities in non-contractual settings.