Machine Learning for Set-Identified Linear Models

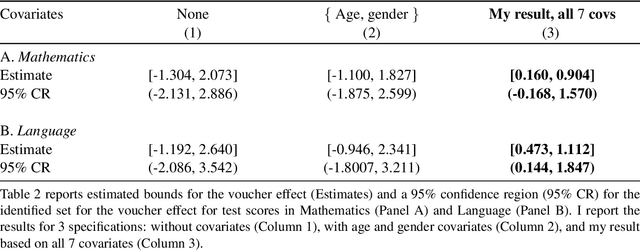
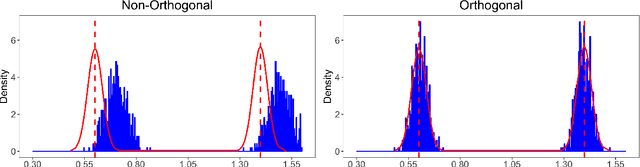
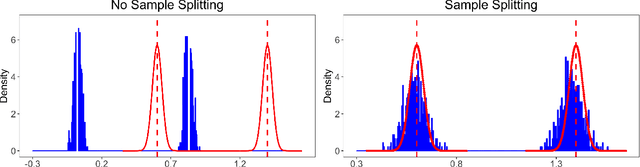
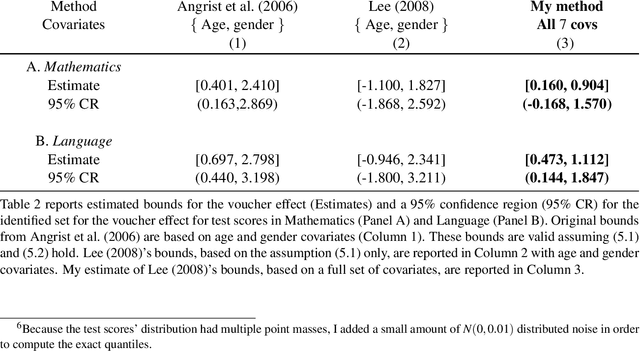
Set-identified models often restrict the number of covariates leading to wide identified sets in practice. This paper provides estimation and inference methods for set-identified linear models with high-dimensional covariates where the model selection is based on modern machine learning tools. I characterize the boundary (i.e, support function) of the identified set using a semiparametric moment condition. Combining Neyman-orthogonality and sample splitting ideas, I construct a root-N consistent, the uniformly asymptotically Gaussian estimator of the support function. I also prove the validity of the Bayesian bootstrap procedure to conduct inference about the identified set. I provide a general method to construct a Neyman-orthogonal moment condition for the support function. I apply this result to estimate sharp nonparametric bounds on the average treatment effect in Lee (2008)'s model of endogenous selection and substantially tighten the bounds on this parameter in Angrist et al. (2006)'s empirical setting. I also apply this result to estimate sharp identified sets for two other parameters - a new parameter, called a partially linear predictor, and the average partial derivative when the outcome variable is recorded in intervals.