Inference on weighted average value function in high-dimensional state space

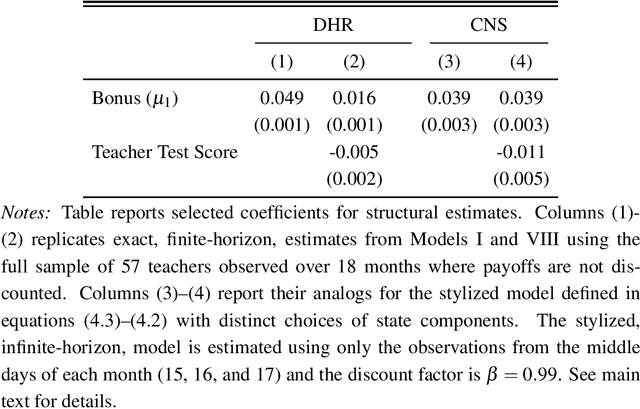
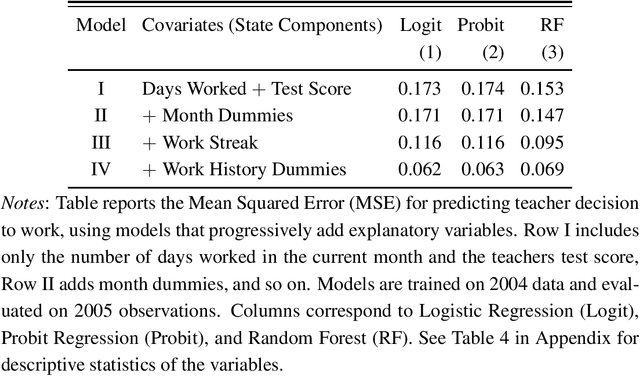
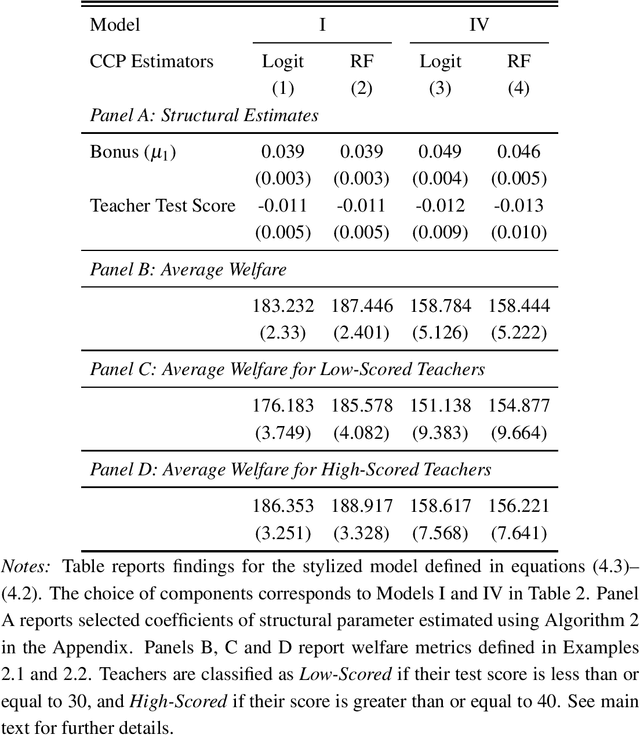
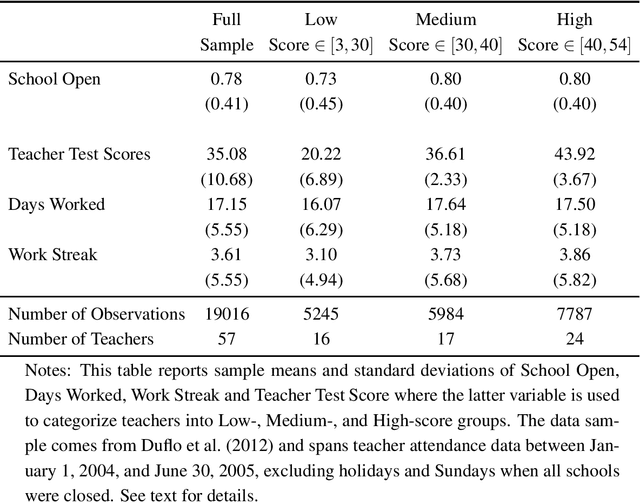
This paper gives a consistent, asymptotically normal estimator of the expected value function when the state space is high-dimensional and the first-stage nuisance functions are estimated by modern machine learning tools. First, we show that value function is orthogonal to the conditional choice probability, therefore, this nuisance function needs to be estimated only at $n^{-1/4}$ rate. Second, we give a correction term for the transition density of the state variable. The resulting orthogonal moment is robust to misspecification of the transition density and does not require this nuisance function to be consistently estimated. Third, we generalize this result by considering the weighted expected value. In this case, the orthogonal moment is doubly robust in the transition density and additional second-stage nuisance functions entering the correction term. We complete the asymptotic theory by providing bounds on second-order asymptotic terms.