Matt Goldman
Machine Learning for Variance Reduction in Online Experiments
Jun 16, 2021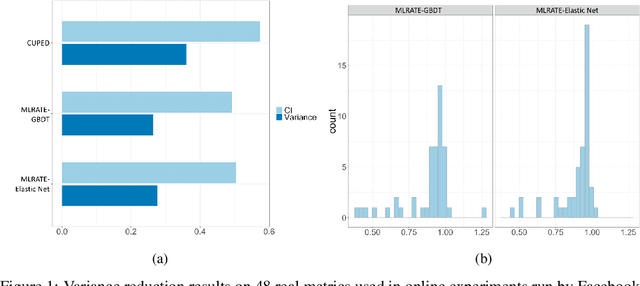
Abstract:We consider the problem of variance reduction in randomized controlled trials, through the use of covariates correlated with the outcome but independent of the treatment. We propose a machine learning regression-adjusted treatment effect estimator, which we call MLRATE. MLRATE uses machine learning predictors of the outcome to reduce estimator variance. It employs cross-fitting to avoid overfitting biases, and we prove consistency and asymptotic normality under general conditions. MLRATE is robust to poor predictions from the machine learning step: if the predictions are uncorrelated with the outcomes, the estimator performs asymptotically no worse than the standard difference-in-means estimator, while if predictions are highly correlated with outcomes, the efficiency gains are large. In A/A tests, for a set of 48 outcome metrics commonly monitored in Facebook experiments the estimator has over 70% lower variance than the simple difference-in-means estimator, and about 19% lower variance than the common univariate procedure which adjusts only for pre-experiment values of the outcome.
Matching on What Matters: A Pseudo-Metric Learning Approach to Matching Estimation in High Dimensions
May 28, 2019



Abstract:When pre-processing observational data via matching, we seek to approximate each unit with maximally similar peers that had an alternative treatment status--essentially replicating a randomized block design. However, as one considers a growing number of continuous features, a curse of dimensionality applies making asymptotically valid inference impossible (Abadie and Imbens, 2006). The alternative of ignoring plausibly relevant features is certainly no better, and the resulting trade-off substantially limits the application of matching methods to "wide" datasets. Instead, Li and Fu (2017) recasts the problem of matching in a metric learning framework that maps features to a low-dimensional space that facilitates "closer matches" while still capturing important aspects of unit-level heterogeneity. However, that method lacks key theoretical guarantees and can produce inconsistent estimates in cases of heterogeneous treatment effects. Motivated by straightforward extension of existing results in the matching literature, we present alternative techniques that learn latent matching features through either MLPs or through siamese neural networks trained on a carefully selected loss function. We benchmark the resulting alternative methods in simulations as well as against two experimental data sets--including the canonical NSW worker training program data set--and find superior performance of the neural-net-based methods.
Pricing Engine: Estimating Causal Impacts in Real World Business Settings
Jun 12, 2018
Abstract:We introduce the Pricing Engine package to enable the use of Double ML estimation techniques in general panel data settings. Customization allows the user to specify first-stage models, first-stage featurization, second stage treatment selection and second stage causal-modeling. We also introduce a DynamicDML class that allows the user to generate dynamic treatment-aware forecasts at a range of leads and to understand how the forecasts will vary as a function of causally estimated treatment parameters. The Pricing Engine is built on Python 3.5 and can be run on an Azure ML Workbench environment with the addition of only a few Python packages. This note provides high-level discussion of the Double ML method, describes the packages intended use and includes an example Jupyter notebook demonstrating application to some publicly available data. Installation of the package and additional technical documentation is available at $\href{https://github.com/bquistorff/pricingengine}{github.com/bquistorff/pricingengine}$.
Orthogonal Machine Learning for Demand Estimation: High Dimensional Causal Inference in Dynamic Panels
Jan 10, 2018

Abstract:There has been growing interest in how economists can import machine learning tools designed for prediction to accelerate and automate the model selection process, while still retaining desirable inference properties for causal parameters. Focusing on partially linear models, we extend the Double ML framework to allow for (1) a number of treatments that may grow with the sample size and (2) the analysis of panel data under sequentially exogenous errors. Our low-dimensional treatment (LD) regime directly extends the work in [Chernozhukov et al., 2016], by showing that the coefficients from a second stage, ordinary least squares estimator attain root-n convergence and desired coverage even if the dimensionality of treatment is allowed to grow. In a high-dimensional sparse (HDS) regime, we show that second stage LASSO and debiased LASSO have asymptotic properties equivalent to oracle estimators with no upstream error. We argue that these advances make Double ML methods a desirable alternative for practitioners estimating short-term demand elasticities in non-contractual settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge