MiWaves Reinforcement Learning Algorithm

The escalating prevalence of cannabis use poses a significant public health challenge globally. In the U.S., cannabis use is more prevalent among emerging adults (EAs) (ages 18-25) than any other age group, with legalization in the multiple states contributing to a public perception that cannabis is less risky than in prior decades. To address this growing concern, we developed MiWaves, a reinforcement learning (RL) algorithm designed to optimize the delivery of personalized intervention prompts to reduce cannabis use among EAs. MiWaves leverages domain expertise and prior data to tailor the likelihood of delivery of intervention messages. This paper presents a comprehensive overview of the algorithm's design, including key decisions and experimental outcomes. The finalized MiWaves RL algorithm was deployed in a clinical trial from March to May 2024.

reBandit: Random Effects based Online RL algorithm for Reducing Cannabis Use

The escalating prevalence of cannabis use, and associated cannabis-use disorder (CUD), poses a significant public health challenge globally. With a notably wide treatment gap, especially among emerging adults (EAs; ages 18-25), addressing cannabis use and CUD remains a pivotal objective within the 2030 United Nations Agenda for Sustainable Development Goals (SDG). In this work, we develop an online reinforcement learning (RL) algorithm called reBandit which will be utilized in a mobile health study to deliver personalized mobile health interventions aimed at reducing cannabis use among EAs. reBandit utilizes random effects and informative Bayesian priors to learn quickly and efficiently in noisy mobile health environments. Moreover, reBandit employs Empirical Bayes and optimization techniques to autonomously update its hyper-parameters online. To evaluate the performance of our algorithm, we construct a simulation testbed using data from a prior study, and compare against commonly used algorithms in mobile health studies. We show that reBandit performs equally well or better than all the baseline algorithms, and the performance gap widens as population heterogeneity increases in the simulation environment, proving its adeptness to adapt to diverse population of study participants.

Online learning in bandits with predicted context

We consider the contextual bandit problem where at each time, the agent only has access to a noisy version of the context and the error variance (or an estimator of this variance). This setting is motivated by a wide range of applications where the true context for decision-making is unobserved, and only a prediction of the context by a potentially complex machine learning algorithm is available. When the context error is non-diminishing, classical bandit algorithms fail to achieve sublinear regret. We propose the first online algorithm in this setting with sublinear regret compared to the appropriate benchmark. The key idea is to extend the measurement error model in classical statistics to the online decision-making setting, which is nontrivial due to the policy being dependent on the noisy context observations.

Policy Optimization Using Semiparametric Models for Dynamic Pricing

In this paper, we study the contextual dynamic pricing problem where the market value of a product is linear in its observed features plus some market noise. Products are sold one at a time, and only a binary response indicating success or failure of a sale is observed. Our model setting is similar to Javanmard and Nazerzadeh [2019] except that we expand the demand curve to a semiparametric model and need to learn dynamically both parametric and nonparametric components. We propose a dynamic statistical learning and decision-making policy that combines semiparametric estimation from a generalized linear model with an unknown link and online decision-making to minimize regret (maximize revenue). Under mild conditions, we show that for a market noise c.d.f. $F(\cdot)$ with $m$-th order derivative ($m\geq 2$), our policy achieves a regret upper bound of $\tilde{O}_{d}(T^{\frac{2m+1}{4m-1}})$, where $T$ is time horizon and $\tilde{O}_{d}$ is the order that hides logarithmic terms and the dimensionality of feature $d$. The upper bound is further reduced to $\tilde{O}_{d}(\sqrt{T})$ if $F$ is super smooth whose Fourier transform decays exponentially. In terms of dependence on the horizon $T$, these upper bounds are close to $\Omega(\sqrt{T})$, the lower bound where $F$ belongs to a parametric class. We further generalize these results to the case with dynamically dependent product features under the strong mixing condition.

Machine Learning for Variance Reduction in Online Experiments

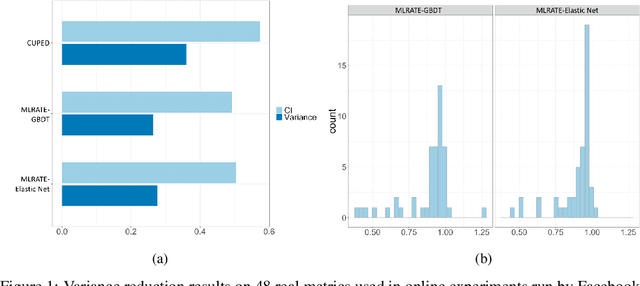
We consider the problem of variance reduction in randomized controlled trials, through the use of covariates correlated with the outcome but independent of the treatment. We propose a machine learning regression-adjusted treatment effect estimator, which we call MLRATE. MLRATE uses machine learning predictors of the outcome to reduce estimator variance. It employs cross-fitting to avoid overfitting biases, and we prove consistency and asymptotic normality under general conditions. MLRATE is robust to poor predictions from the machine learning step: if the predictions are uncorrelated with the outcomes, the estimator performs asymptotically no worse than the standard difference-in-means estimator, while if predictions are highly correlated with outcomes, the efficiency gains are large. In A/A tests, for a set of 48 outcome metrics commonly monitored in Facebook experiments the estimator has over 70% lower variance than the simple difference-in-means estimator, and about 19% lower variance than the common univariate procedure which adjusts only for pre-experiment values of the outcome.

Communication-Efficient Accurate Statistical Estimation

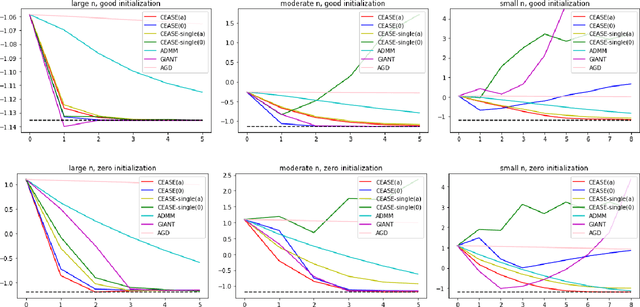
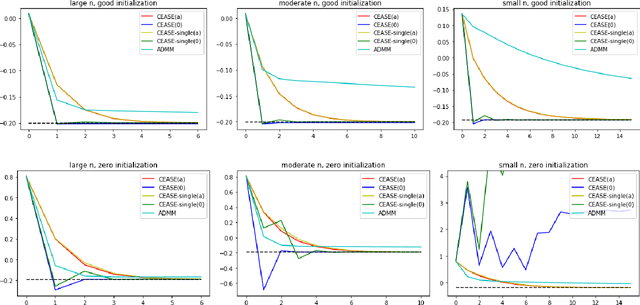
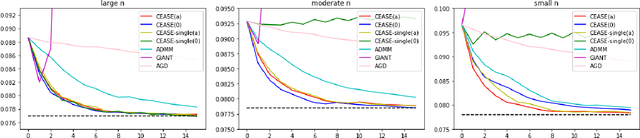
When the data are stored in a distributed manner, direct application of traditional statistical inference procedures is often prohibitive due to communication cost and privacy concerns. This paper develops and investigates two Communication-Efficient Accurate Statistical Estimators (CEASE), implemented through iterative algorithms for distributed optimization. In each iteration, node machines carry out computation in parallel and communicate with the central processor, which then broadcasts aggregated information to node machines for new updates. The algorithms adapt to the similarity among loss functions on node machines, and converge rapidly when each node machine has large enough sample size. Moreover, they do not require good initialization and enjoy linear converge guarantees under general conditions. The contraction rate of optimization errors is presented explicitly, with dependence on the local sample size unveiled. In addition, the improved statistical accuracy per iteration is derived. By regarding the proposed method as a multi-step statistical estimator, we show that statistical efficiency can be achieved in finite steps in typical statistical applications. In addition, we give the conditions under which the one-step CEASE estimator is statistically efficient. Extensive numerical experiments on both synthetic and real data validate the theoretical results and demonstrate the superior performance of our algorithms.