Simultaneous Inference for Best Linear Predictor of the Conditional Average Treatment Effect and Other Structural Functions

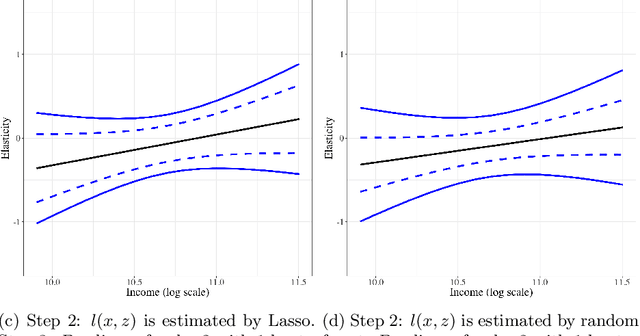
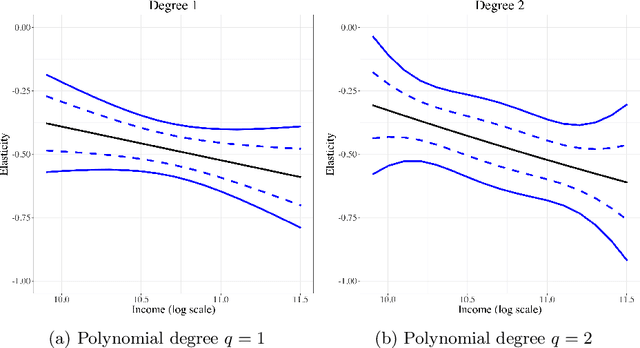
This paper provides estimation and inference methods for a structural function, such as Conditional Average Treatment Effect (CATE), based on modern machine learning (ML) tools. We assume that such function can be represented as an expectation g(x) of a signal Y conditional on X that depends on an unknown nuisance function. In addition to CATE, examples of such functions include regression function with Partially Missing Outcome and Conditional Average Partial Derivative. We approximate g(x) by a linear form that is a product of a vector of the approximating basis functions p(x) and the Best Linear Predictor (BLP), which we refer to a pseudo-target. Plugging in the first-stage estimate of the nuisance function into the signal, we estimate BLP via ordinary least squares. We deliver a high-quality estimate of the pseudo-target function that features (a) a pointwise Gaussian approximation, (b) a simultaneous Gaussian approximation, and (c) optimal rate of simultaneous convergence. In the case, the misspecification error of the linear form decays sufficiently fast, these approximations automatically hold for the target function g(x) instead of a pseudo-target. The first stage nuisance parameter is allowed to be high-dimensional and is estimated by modern ML tools, such as neural networks, shrinkage estimators, and random forest. Using our method, we estimate the average price elasticity conditional on income using Yatchew and No (2001) data and provide simultaneous confidence bands for the target regression function.