How Bad is Top-$K$ Recommendation under Competing Content Creators?

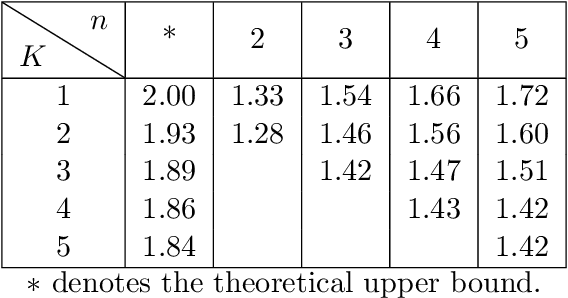
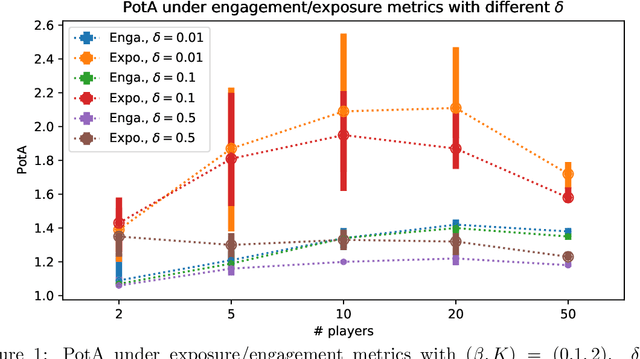
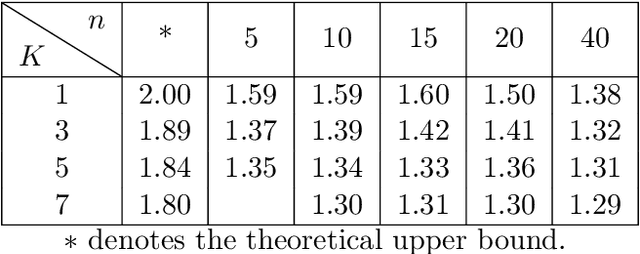
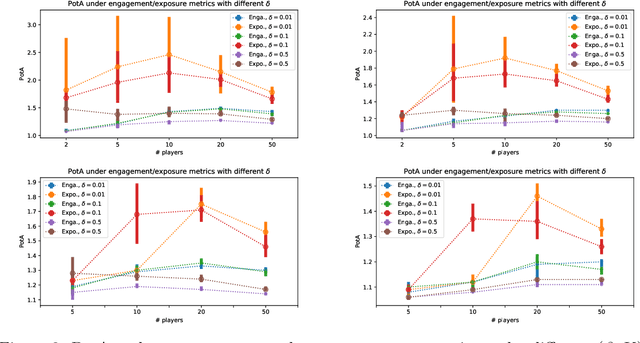
Content creators compete for exposure on recommendation platforms, and such strategic behavior leads to a dynamic shift over the content distribution. However, how the creators' competition impacts user welfare and how the relevance-driven recommendation influences the dynamics in the long run are still largely unknown. This work provides theoretical insights into these research questions. We model the creators' competition under the assumptions that: 1) the platform employs an innocuous top-$K$ recommendation policy; 2) user decisions follow the Random Utility model; 3) content creators compete for user engagement and, without knowing their utility function in hindsight, apply arbitrary no-regret learning algorithms to update their strategies. We study the user welfare guarantee through the lens of Price of Anarchy and show that the fraction of user welfare loss due to creator competition is always upper bounded by a small constant depending on $K$ and randomness in user decisions; we also prove the tightness of this bound. Our result discloses an intrinsic merit of the myopic approach to the recommendation, i.e., relevance-driven matching performs reasonably well in the long run, as long as users' decisions involve randomness and the platform provides reasonably many alternatives to its users.

Learning from a Learning User for Optimal Recommendations

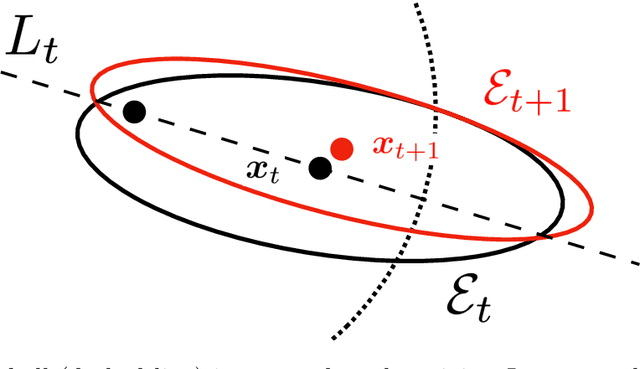
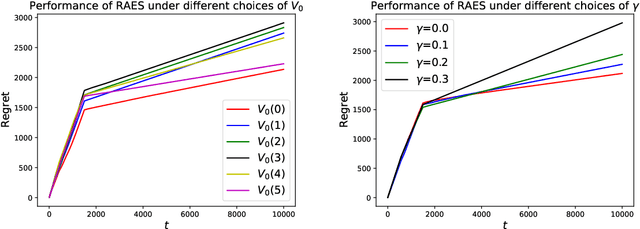
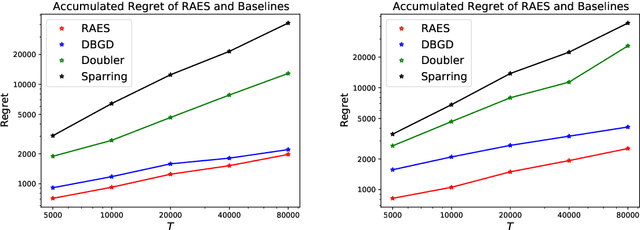
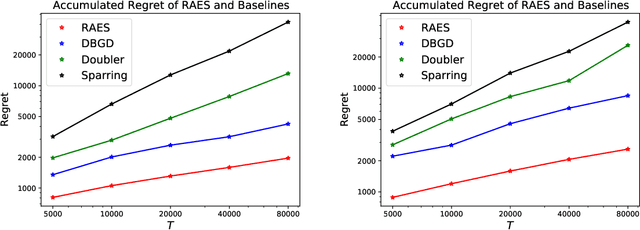
In real-world recommendation problems, especially those with a formidably large item space, users have to gradually learn to estimate the utility of any fresh recommendations from their experience about previously consumed items. This in turn affects their interaction dynamics with the system and can invalidate previous algorithms built on the omniscient user assumption. In this paper, we formalize a model to capture such "learning users" and design an efficient system-side learning solution, coined Noise-Robust Active Ellipsoid Search (RAES), to confront the challenges brought by the non-stationary feedback from such a learning user. Interestingly, we prove that the regret of RAES deteriorates gracefully as the convergence rate of user learning becomes worse, until reaching linear regret when the user's learning fails to converge. Experiments on synthetic datasets demonstrate the strength of RAES for such a contemporaneous system-user learning problem. Our study provides a novel perspective on modeling the feedback loop in recommendation problems.

Learning the Optimal Recommendation from Explorative Users

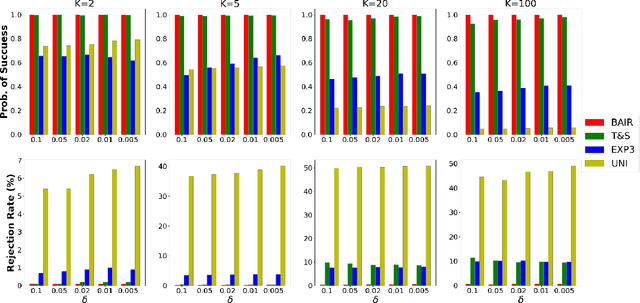
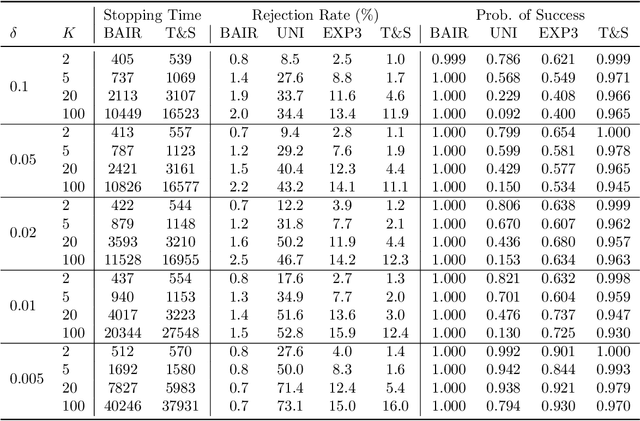
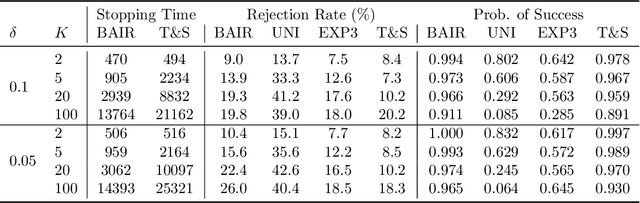
We propose a new problem setting to study the sequential interactions between a recommender system and a user. Instead of assuming the user is omniscient, static, and explicit, as the classical practice does, we sketch a more realistic user behavior model, under which the user: 1) rejects recommendations if they are clearly worse than others; 2) updates her utility estimation based on rewards from her accepted recommendations; 3) withholds realized rewards from the system. We formulate the interactions between the system and such an explorative user in a $K$-armed bandit framework and study the problem of learning the optimal recommendation on the system side. We show that efficient system learning is still possible but is more difficult. In particular, the system can identify the best arm with probability at least $1-\delta$ within $O(1/\delta)$ interactions, and we prove this is tight. Our finding contrasts the result for the problem of best arm identification with fixed confidence, in which the best arm can be identified with probability $1-\delta$ within $O(\log(1/\delta))$ interactions. This gap illustrates the inevitable cost the system has to pay when it learns from an explorative user's revealed preferences on its recommendations rather than from the realized rewards.

Plug-in Regularized Estimation of High-Dimensional Parameters in Nonlinear Semiparametric Models

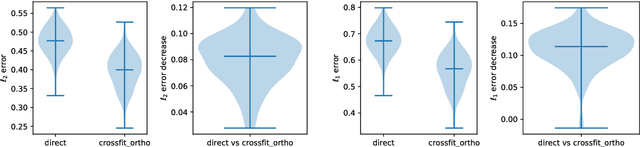
We develop a theory for estimation of a high-dimensional sparse parameter $\theta$ defined as a minimizer of a population loss function $L_D(\theta,g_0)$ which, in addition to $\theta$, depends on a, potentially infinite dimensional, nuisance parameter $g_0$. Our approach is based on estimating $\theta$ via an $\ell_1$-regularized minimization of a sample analog of $L_S(\theta, \hat{g})$, plugging in a first-stage estimate $\hat{g}$, computed on a hold-out sample. We define a population loss to be (Neyman) orthogonal if the gradient of the loss with respect to $\theta$, has pathwise derivative with respect to $g$ equal to zero, when evaluated at the true parameter and nuisance component. We show that orthogonality implies a second-order impact of the first stage nuisance error on the second stage target parameter estimate. Our approach applies to both convex and non-convex losses, albeit the latter case requires a small adaptation of our method with a preliminary estimation step of the target parameter. Our result enables oracle convergence rates for $\theta$ under assumptions on the first stage rates, typically of the order of $n^{-1/4}$. We show how such an orthogonal loss can be constructed via a novel orthogonalization process for a general model defined by conditional moment restrictions. We apply our theory to high-dimensional versions of standard estimation problems in statistics and econometrics, such as: estimation of conditional moment models with missing data, estimation of structural utilities in games of incomplete information and estimation of treatment effects in regression models with non-linear link functions.