Learning the Optimal Recommendation from Explorative Users
Paper and Code
Oct 06, 2021
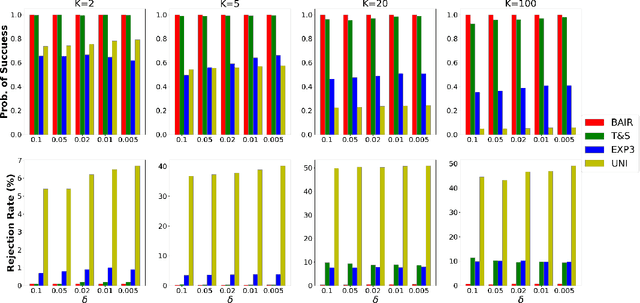
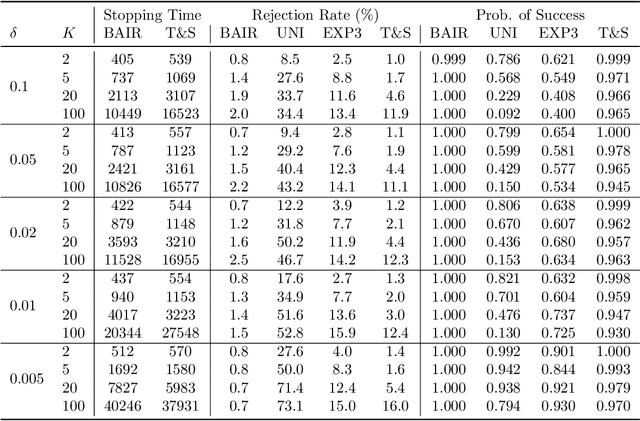
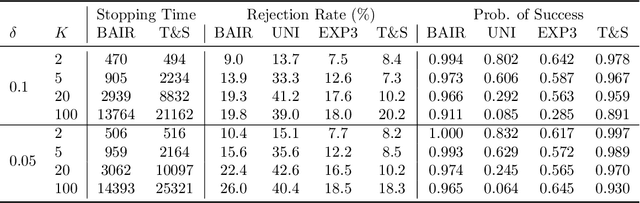
We propose a new problem setting to study the sequential interactions between a recommender system and a user. Instead of assuming the user is omniscient, static, and explicit, as the classical practice does, we sketch a more realistic user behavior model, under which the user: 1) rejects recommendations if they are clearly worse than others; 2) updates her utility estimation based on rewards from her accepted recommendations; 3) withholds realized rewards from the system. We formulate the interactions between the system and such an explorative user in a $K$-armed bandit framework and study the problem of learning the optimal recommendation on the system side. We show that efficient system learning is still possible but is more difficult. In particular, the system can identify the best arm with probability at least $1-\delta$ within $O(1/\delta)$ interactions, and we prove this is tight. Our finding contrasts the result for the problem of best arm identification with fixed confidence, in which the best arm can be identified with probability $1-\delta$ within $O(\log(1/\delta))$ interactions. This gap illustrates the inevitable cost the system has to pay when it learns from an explorative user's revealed preferences on its recommendations rather than from the realized rewards.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge