THE-SEAN: A Heart Rate Variation-Inspired Temporally High-Order Event-Based Visual Odometry with Self-Supervised Spiking Event Accumulation Networks

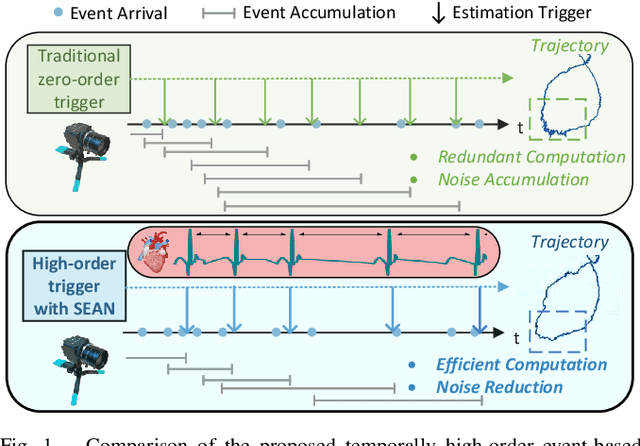
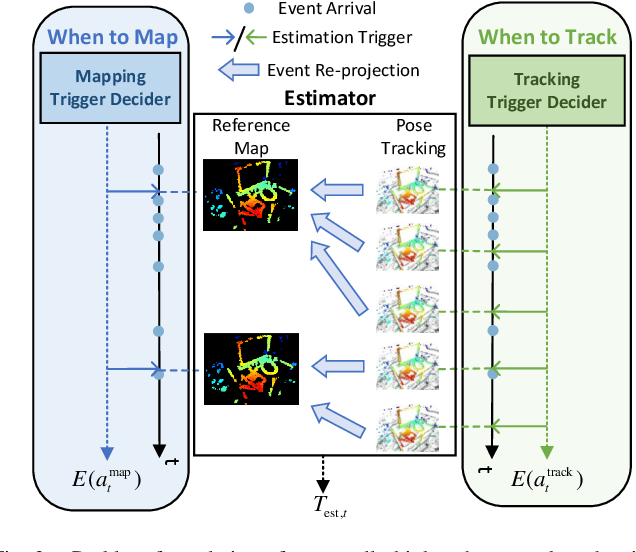
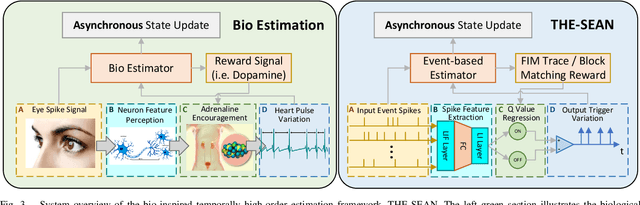
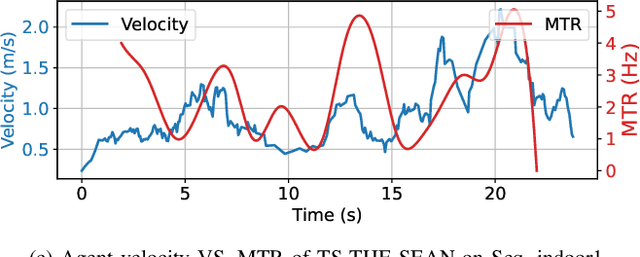
Event-based visual odometry has recently gained attention for its high accuracy and real-time performance in fast-motion systems. Unlike traditional synchronous estimators that rely on constant-frequency (zero-order) triggers, event-based visual odometry can actively accumulate information to generate temporally high-order estimation triggers. However, existing methods primarily focus on adaptive event representation after estimation triggers, neglecting the decision-making process for efficient temporal triggering itself. This oversight leads to the computational redundancy and noise accumulation. In this paper, we introduce a temporally high-order event-based visual odometry with spiking event accumulation networks (THE-SEAN). To the best of our knowledge, it is the first event-based visual odometry capable of dynamically adjusting its estimation trigger decision in response to motion and environmental changes. Inspired by biological systems that regulate hormone secretion to modulate heart rate, a self-supervised spiking neural network is designed to generate estimation triggers. This spiking network extracts temporal features to produce triggers, with rewards based on block matching points and Fisher information matrix (FIM) trace acquired from the estimator itself. Finally, THE-SEAN is evaluated across several open datasets, thereby demonstrating average improvements of 13\% in estimation accuracy, 9\% in smoothness, and 38\% in triggering efficiency compared to the state-of-the-art methods.

General Method for Prime-point Cyclic Convolution over the Real Field

A general and fast method is conceived for computing the cyclic convolution of n points, where n is a prime number. This method fully exploits the internal structure of the cyclic matrix, and hence leads to significant reduction of the multiplication complexity in terms of CPU time by 50%, as compared with Winograd's algorithm. In this paper, we only consider the real and complex fields due to their most important applications, but in general, the idea behind this method can be extended to any finite field of interest. Clearly, it is well-known that the discrete Fourier transform (DFT) can be expressed in terms of cyclic convolution, so it can be utilized to compute the DFT when the block length is a prime.

Matrix Completion via Nonconvex Regularization: Convergence of the Proximal Gradient Algorithm

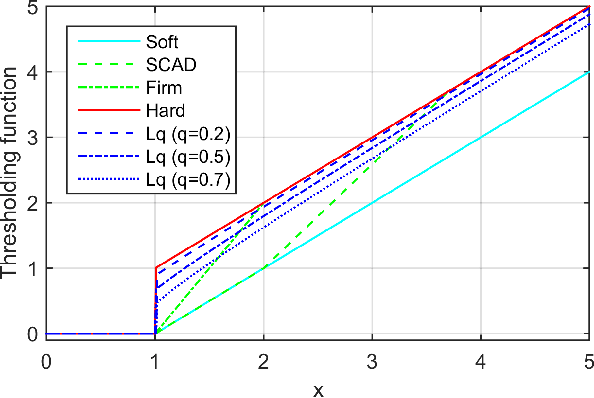
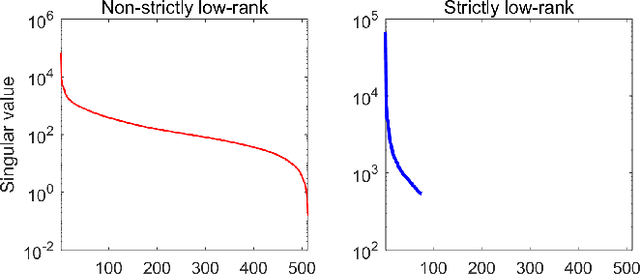
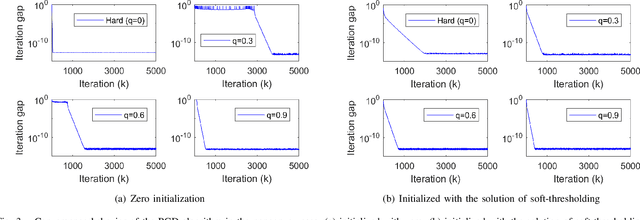
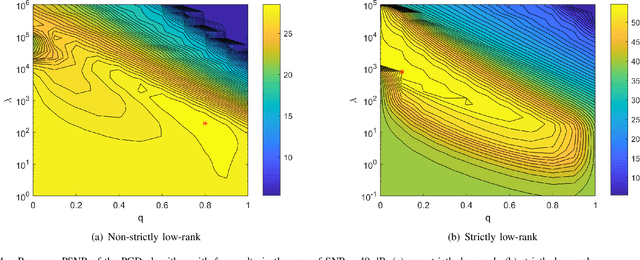
Matrix completion has attracted much interest in the past decade in machine learning and computer vision. For low-rank promotion in matrix completion, the nuclear norm penalty is convenient due to its convexity but has a bias problem. Recently, various algorithms using nonconvex penalties have been proposed, among which the proximal gradient descent (PGD) algorithm is one of the most efficient and effective. For the nonconvex PGD algorithm, whether it converges to a local minimizer and its convergence rate are still unclear. This work provides a nontrivial analysis on the PGD algorithm in the nonconvex case. Besides the convergence to a stationary point for a generalized nonconvex penalty, we provide more deep analysis on a popular and important class of nonconvex penalties which have discontinuous thresholding functions. For such penalties, we establish the finite rank convergence, convergence to restricted strictly local minimizer and eventually linear convergence rate of the PGD algorithm. Meanwhile, convergence to a local minimizer has been proved for the hard-thresholding penalty. Our result is the first shows that, nonconvex regularized matrix completion only has restricted strictly local minimizers, and the PGD algorithm can converge to such minimizers with eventually linear rate under certain conditions. Illustration of the PGD algorithm via experiments has also been provided. Code is available at https://github.com/FWen/nmc.