How Much Power Must We Extract From a Receiver Antenna to Effect Communications?

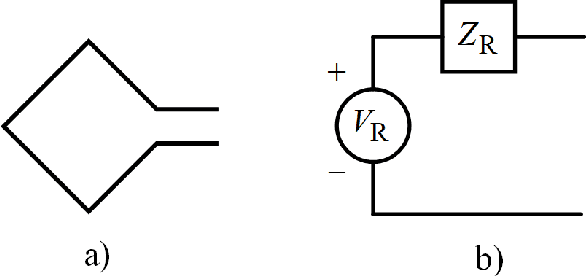
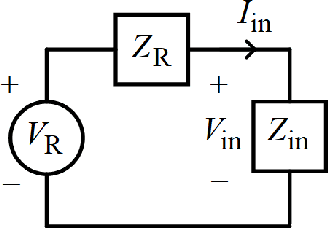
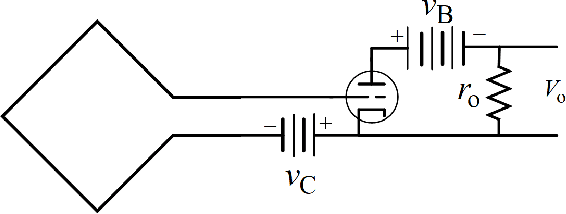
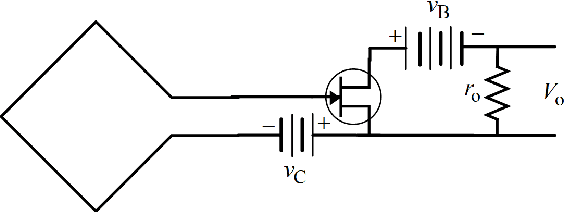
Subject to the laws of classical physics - the science that governs the design of today's wireless communication systems - there is no need to extract power from a receiver antenna in order to effect communications. If we dispense with a transmission line and, instead, make the front-end electronics colocated with the antenna, then a high input-impedance preamplifier can measure the open-circuit voltage directly on the antenna port without drawing either current or power. Neither Friis' concept of noise figure, nor Shannon information theory, nor electronics technology dictates that we must extract power from an antenna.

Towards 6G MIMO: Massive Spatial Multiplexing, Dense Arrays, and Interplay Between Electromagnetics and Processing

The increasing demand for wireless data transfer has been the driving force behind the widespread adoption of Massive MIMO (multiple-input multiple-output) technology in 5G. The next-generation MIMO technology is now being developed to cater to the new data traffic and performance expectations generated by new user devices and services in the next decade. The evolution towards "ultra-massive MIMO (UM-MIMO)" is not only about adding more antennas but will also uncover new propagation and hardware phenomena that can only be treated by jointly utilizing insights from the communication, electromagnetic (EM), and circuit theory areas. This article offers a comprehensive overview of the key benefits of the UM-MIMO technology and the associated challenges. It explores massive multiplexing facilitated by radiative near-field effects, characterizes the spatial degrees-of-freedom, and practical channel estimation schemes tailored for massive arrays. Moreover, we provide a tutorial on EM theory and circuit theory, and how it is used to obtain physically consistent antenna and channel models. Subsequently, the article describes different ways to implement massive and dense antenna arrays, and how to co-design antennas with signal processing. The main open research challenges are identified at the end.

Coupling Matrix-based Beamforming for Superdirective Antenna Arrays

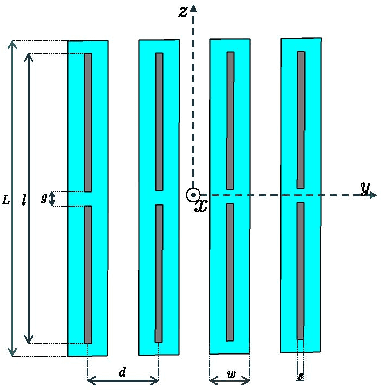
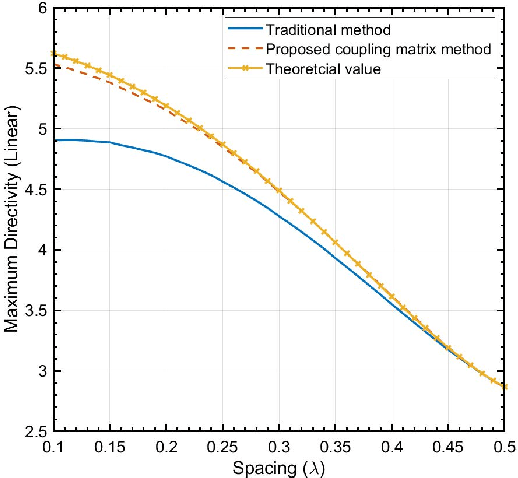
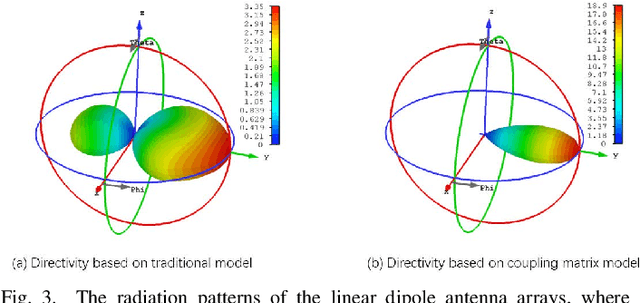
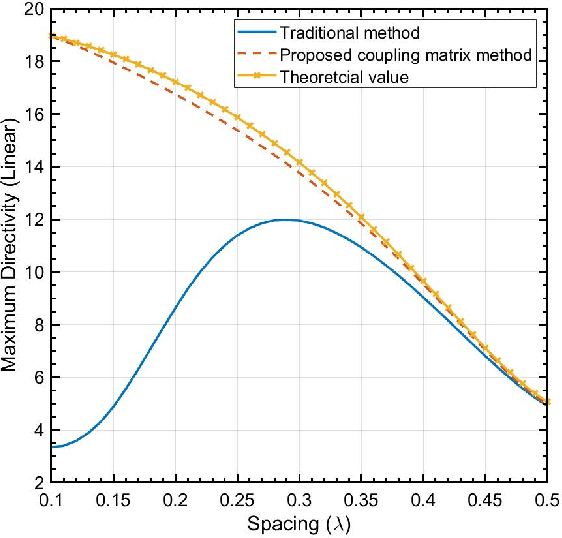
In most multiple-input multiple-output (MIMO) communication systems, e.g., Massive MIMO, the antenna spacing is generally no less than half a wavelength. It helps to reduce the mutual coupling and therefore facilitate the system design. The maximum array gain is the number of antennas in this settings. However, when the antenna spacing is made very small, the array gain of a compact array can be proportional to the square of the number of antennas - a value much larger than the traditional array. To achieve this so-called "superdirectivity" however, the calculation of the excitation coefficients (beamforming vector) is known to be a challenging problem. In this paper, we derive the beamforming vector of superdirective arrays based on a novel coupling matrix-enabled method. We also propose an approach to obtain the coupling matrix, which is derived by the spherical wave expansion method and active element pattern. The full-wave electromagnetic simulations are conducted to validate the effectiveness of our proposed method. Simulation results show that when the beamforming vector obtained by our method is applied, the directivity of the designed dipole antenna array has a good agreement with the theoretical values.

MRT-based Joint Unicast and Multigroup Multicast Transmission in Massive MIMO Systems

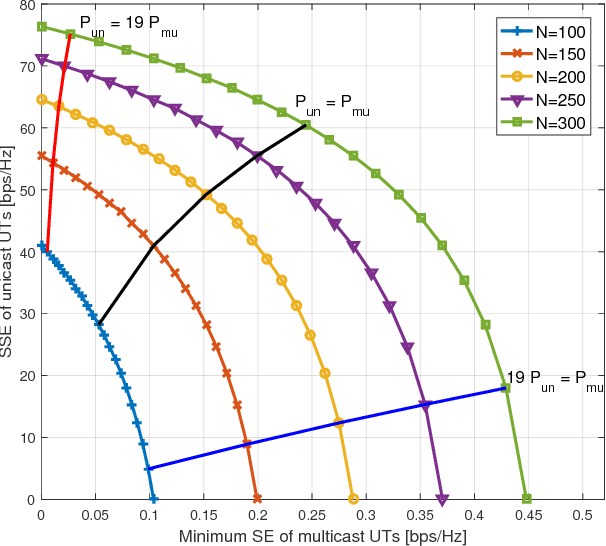
We study joint unicast and multigroup multicast transmission in single-cell massive multiple-input-multiple-output (MIMO) systems, under maximum ratio transmission. For the unicast transmission, the objective is to maximize the weighted sum spectral efficiency (SE) of the unicast user terminals (UTs) and for the multicast transmission the objective is to maximize the minimum SE of the multicast UTs. These two problems are coupled to each other in a conflicting manner, due to their shared power resource and interference. To address this, we formulate a multiobjective optimization problem (MOOP). We derive the Pareto boundary of the MOOP analytically and determine the values of the system parameters to achieve any desired Pareto optimal point. Moreover, we prove that the Pareto region is convex, hence the system should serve the unicast and multicast UTs at the same time-frequency resource.

Nyquist-Sampling and Degrees of Freedom of Electromagnetic Fields

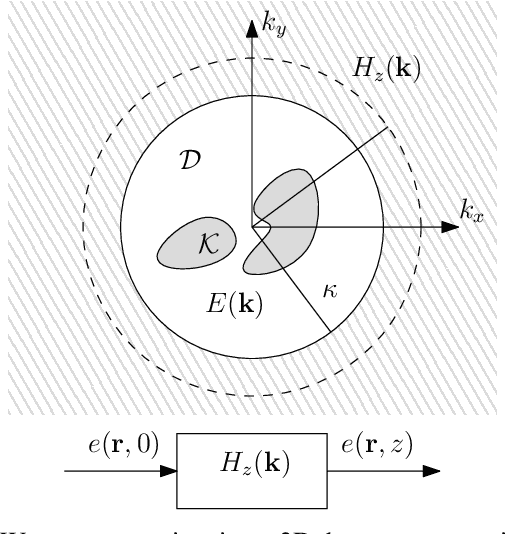
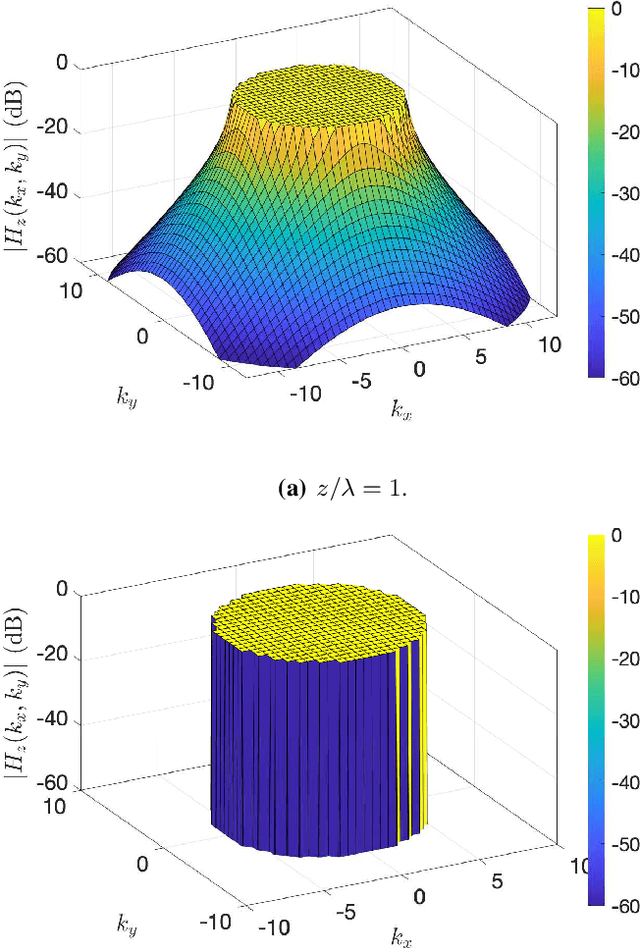
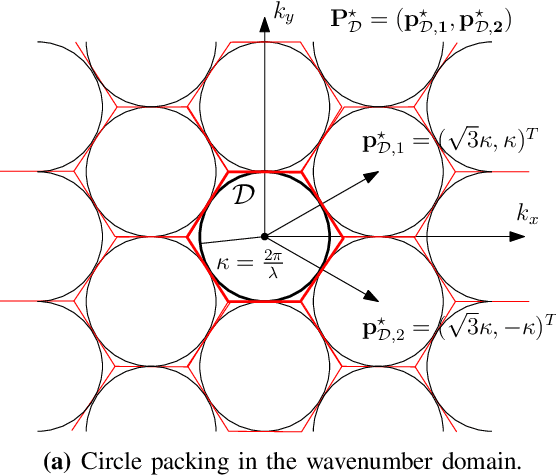
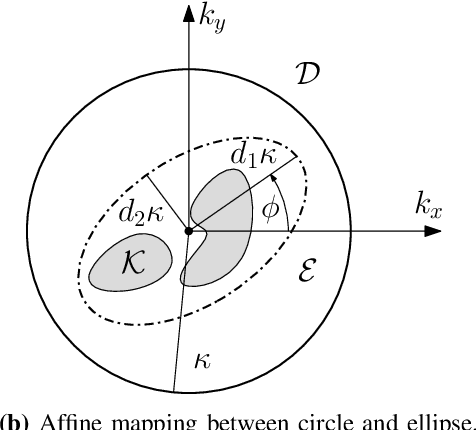
A signal-space approach is presented to study the Nyquist sampling and number of degrees of freedom of an electromagnetic field under arbitrary propagation conditions. Conventional signal processing tools such as the multidimensional sampling theorem and Fourier theory are used to build a linear system theoretic interpretation of electromagnetic wave propagations and revisit classical electromagnetic theory results, e.g., bandlimited property of an electromagnetic field, from a signal processing perspective. Scalar electromagnetic fields are considered for simplicity, which physically correspond to acoustic propagation in general or electromagnetic propagation under certain conditions. The developed approach is extended to study ensembles of a stationary random electromagnetic field that is representative of different propagation conditions.

How Does Cell-Free Massive MIMO Support Multiple Federated Learning Groups?

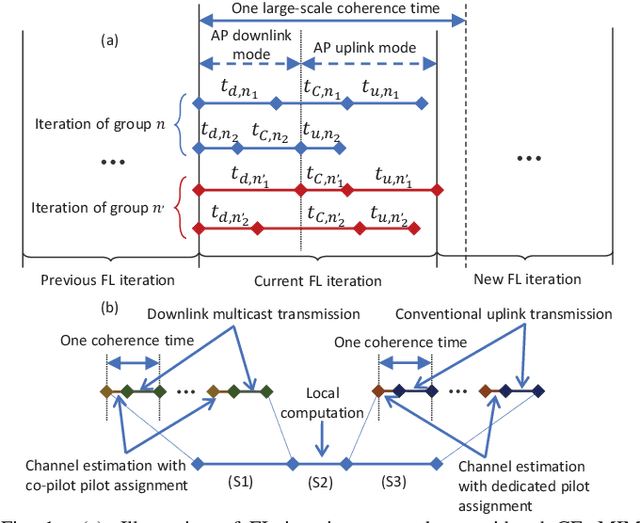
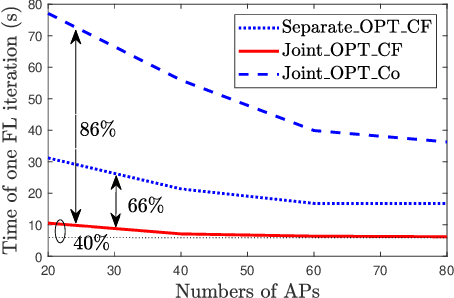
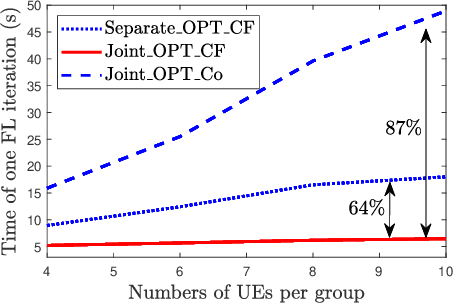
Federated learning (FL) has been considered as a promising learning framework for future machine learning systems due to its privacy preservation and communication efficiency. In beyond-5G/6G systems, it is likely to have multiple FL groups with different learning purposes. This scenario leads to a question: How does a wireless network support multiple FL groups? As an answer, we first propose to use a cell-free massive multiple-input multiple-output (MIMO) network to guarantee the stable operation of multiple FL processes by letting the iterations of these FL processes be executed together within a large-scale coherence time. We then develop a novel scheme that asynchronously executes the iterations of FL processes under multicasting downlink and conventional uplink transmission protocols. Finally, we propose a simple/low-complexity resource allocation algorithm which optimally chooses the power and computation resources to minimize the execution time of each iteration of each FL process.

Holographic MIMO Communications

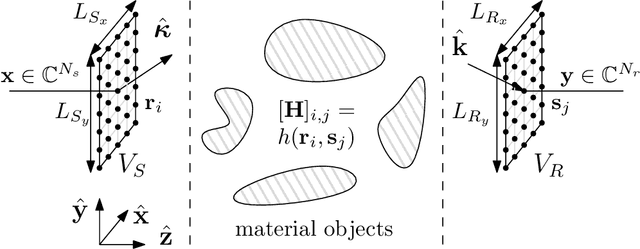
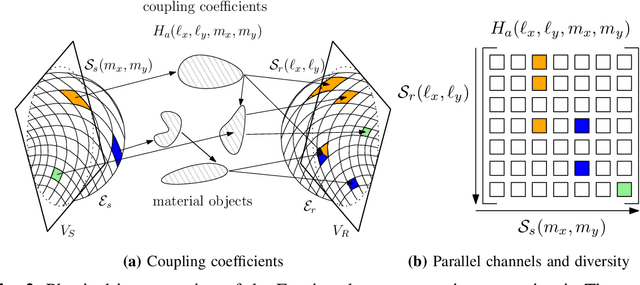
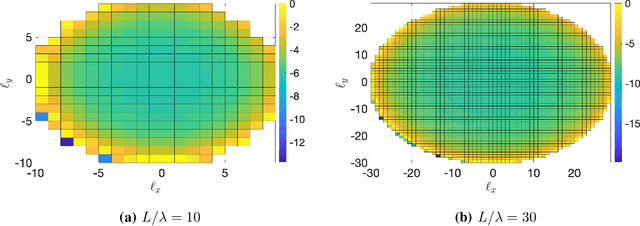
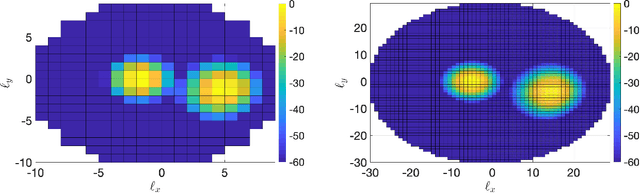
Imagine a MIMO communication system that fully exploits the propagation characteristics offered by an electromagnetic channel and ultimately approaches the limits imposed by wireless communications. This is the concept of Holographic MIMO communications. Accurate and tractable channel modeling is critical to understanding its full potential. Classical stochastic models used by communications theorists are derived under the electromagnetic far-field assumption. However, such assumption breaks down when large (compared to the wavelength) antenna arrays are considered - as envisioned in future wireless communications. In this paper, we start from the first principles of wave propagation and provide a Fourier plane-wave series expansion of the channel response, which fully captures the essence of electromagnetic propagation in arbitrary scattering and is also valid in the (radiative) near-field. The expansion is based on the Fourier spectral representation and has an intuitive physical interpretation, as it statistically describes the angular coupling between source and receiver. When discretized, it leads to a low-rank semi-unitarily equivalent approximation of the spatial electromagnetic channel in the angular domain. The developed channel model is used to compute the ergodic capacity of a Holographic MIMO system with different degrees of channel state information.

Spatial Characterization of Electromagnetic Random Channels

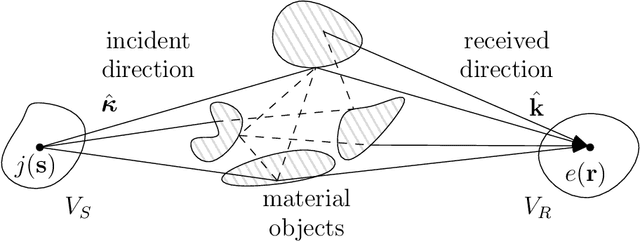
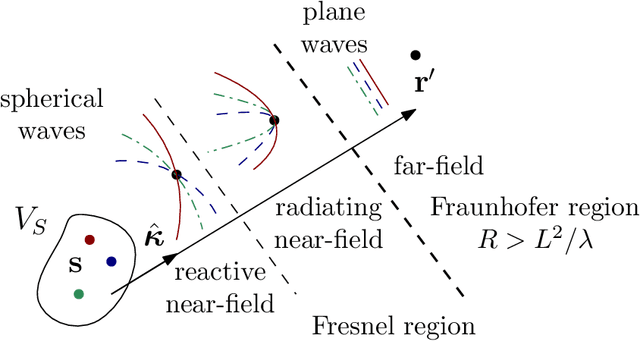
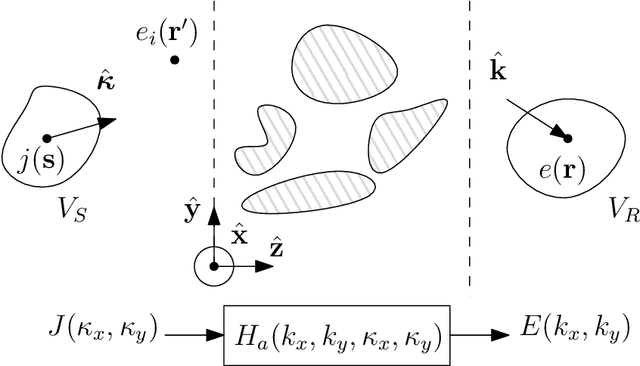
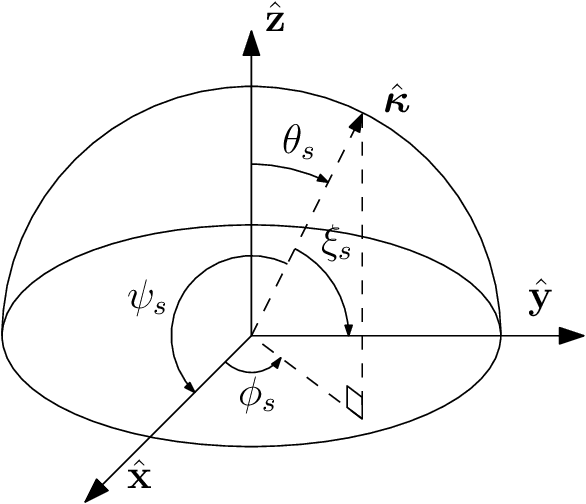
The majority of stochastic channel models rely on the electromagnetic far-field assumption. This assumption breaks down in future applications that push towards the electromagnetic near-field region such as those where the use of very large antenna arrays is envisioned. Motivated by this consideration, we show how physical principles can be used to derive a channel model that is also valid in the electromagnetic near-field. We show that wave propagation through a three-dimensional scattered medium can be generally modeled as a linear and space-variant system. We first review the physics principles that lead to a closed-form deterministic angular representation of the channel response. This serves as a basis for deriving a stochastic representation of the channel in terms of statistically independent Gaussian random coefficients for randomly spatially-stationary propagation environments. The very desirable property of spatial stationarity can always be retained by excluding reactive propagation mechanisms confined in the extreme near-field propagation region. Remarkably, the provided stochastic representation is directly connected to the Fourier spectral representation of a general spatially-stationary random field.