Nyquist-Sampling and Degrees of Freedom of Electromagnetic Fields

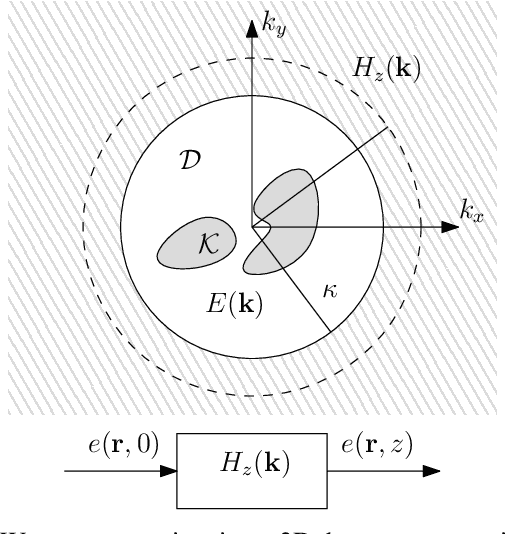
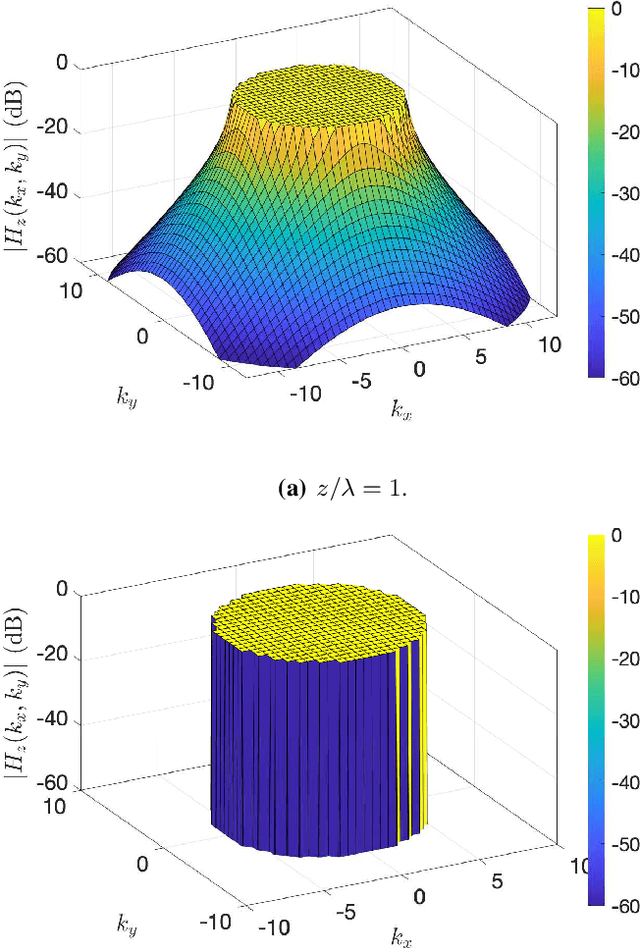
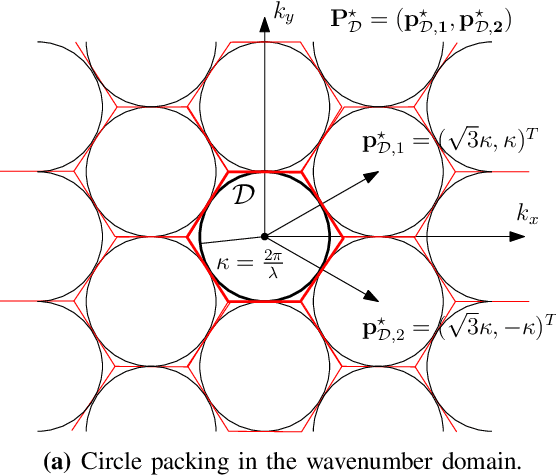
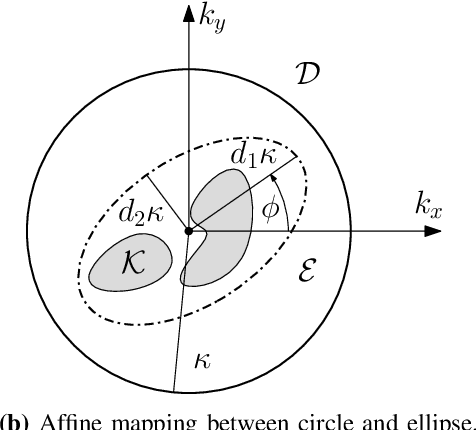
A signal-space approach is presented to study the Nyquist sampling and number of degrees of freedom of an electromagnetic field under arbitrary propagation conditions. Conventional signal processing tools such as the multidimensional sampling theorem and Fourier theory are used to build a linear system theoretic interpretation of electromagnetic wave propagations and revisit classical electromagnetic theory results, e.g., bandlimited property of an electromagnetic field, from a signal processing perspective. Scalar electromagnetic fields are considered for simplicity, which physically correspond to acoustic propagation in general or electromagnetic propagation under certain conditions. The developed approach is extended to study ensembles of a stationary random electromagnetic field that is representative of different propagation conditions.

Holographic MIMO Communications

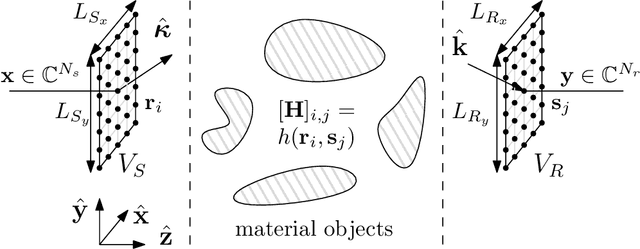
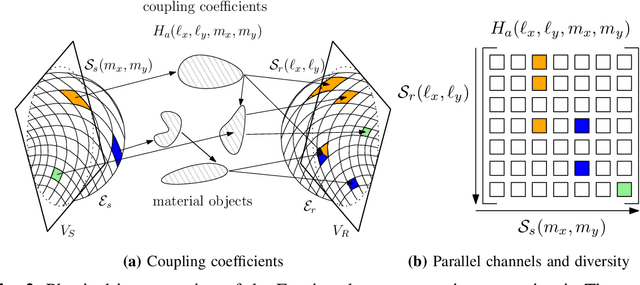
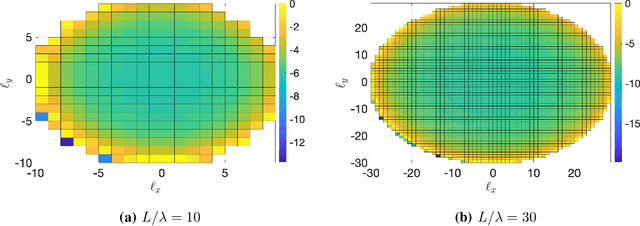
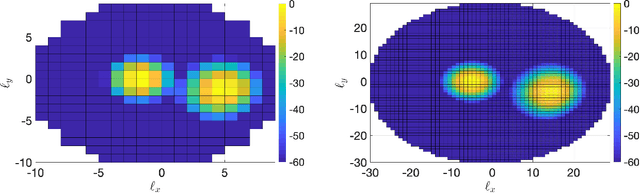
Imagine a MIMO communication system that fully exploits the propagation characteristics offered by an electromagnetic channel and ultimately approaches the limits imposed by wireless communications. This is the concept of Holographic MIMO communications. Accurate and tractable channel modeling is critical to understanding its full potential. Classical stochastic models used by communications theorists are derived under the electromagnetic far-field assumption. However, such assumption breaks down when large (compared to the wavelength) antenna arrays are considered - as envisioned in future wireless communications. In this paper, we start from the first principles of wave propagation and provide a Fourier plane-wave series expansion of the channel response, which fully captures the essence of electromagnetic propagation in arbitrary scattering and is also valid in the (radiative) near-field. The expansion is based on the Fourier spectral representation and has an intuitive physical interpretation, as it statistically describes the angular coupling between source and receiver. When discretized, it leads to a low-rank semi-unitarily equivalent approximation of the spatial electromagnetic channel in the angular domain. The developed channel model is used to compute the ergodic capacity of a Holographic MIMO system with different degrees of channel state information.

Spatial Characterization of Electromagnetic Random Channels

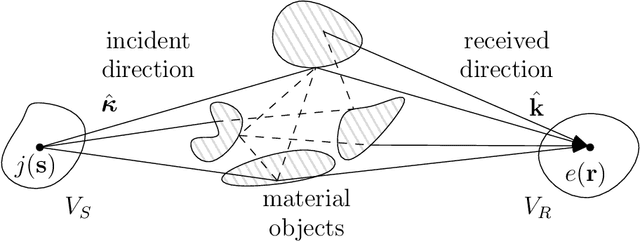
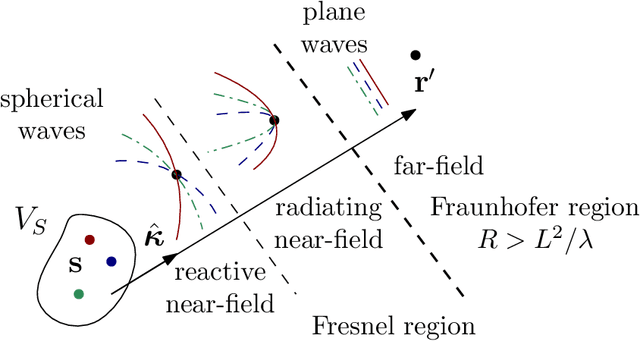
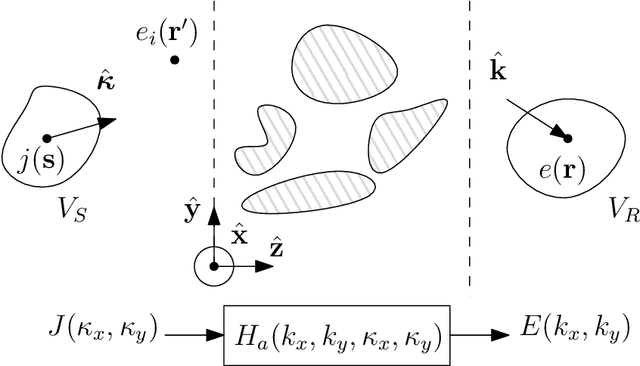
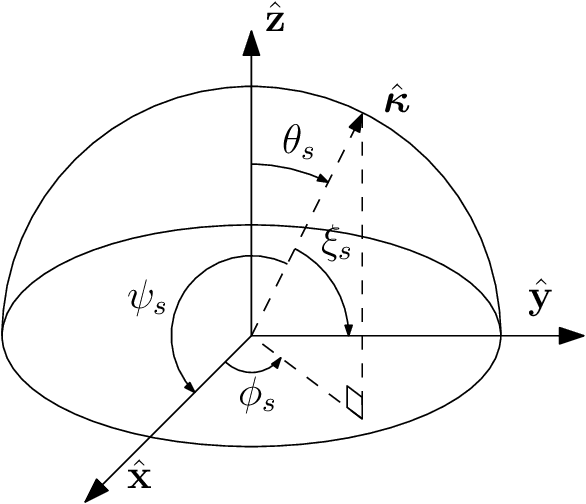
The majority of stochastic channel models rely on the electromagnetic far-field assumption. This assumption breaks down in future applications that push towards the electromagnetic near-field region such as those where the use of very large antenna arrays is envisioned. Motivated by this consideration, we show how physical principles can be used to derive a channel model that is also valid in the electromagnetic near-field. We show that wave propagation through a three-dimensional scattered medium can be generally modeled as a linear and space-variant system. We first review the physics principles that lead to a closed-form deterministic angular representation of the channel response. This serves as a basis for deriving a stochastic representation of the channel in terms of statistically independent Gaussian random coefficients for randomly spatially-stationary propagation environments. The very desirable property of spatial stationarity can always be retained by excluding reactive propagation mechanisms confined in the extreme near-field propagation region. Remarkably, the provided stochastic representation is directly connected to the Fourier spectral representation of a general spatially-stationary random field.