Spatial Characterization of Electromagnetic Random Channels
Paper and Code
Mar 29, 2021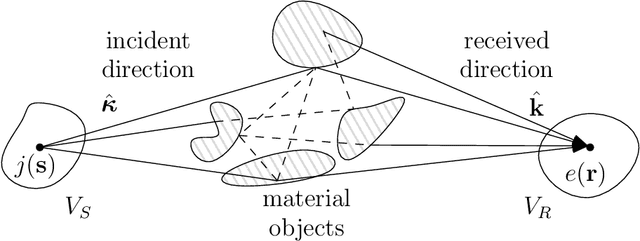
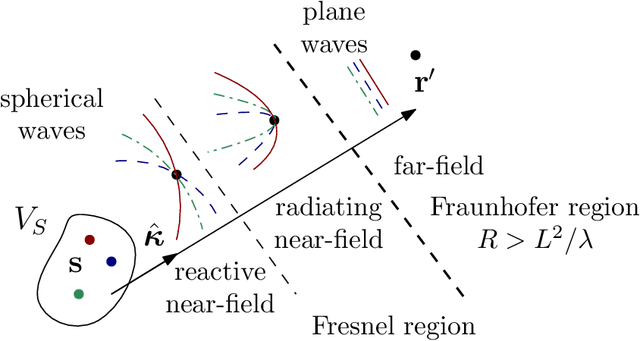
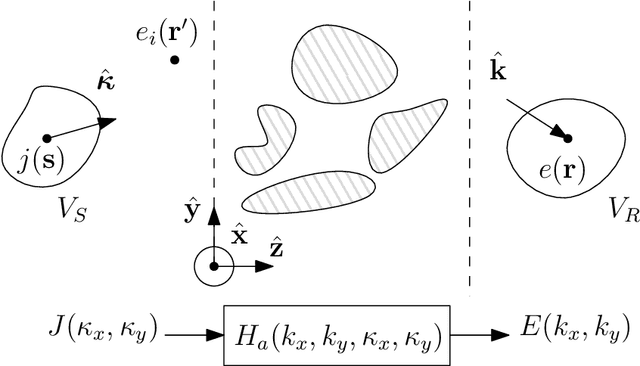
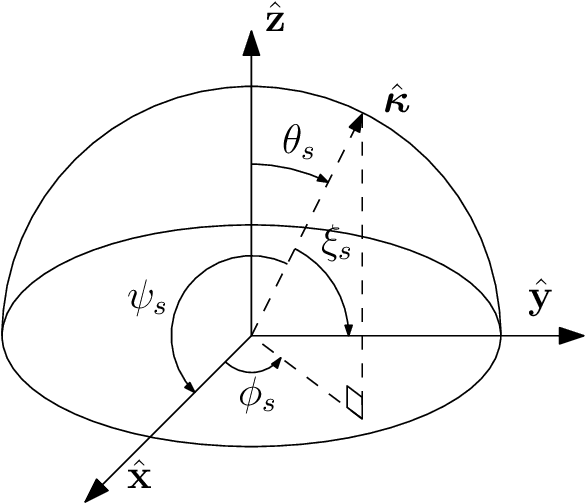
The majority of stochastic channel models rely on the electromagnetic far-field assumption. This assumption breaks down in future applications that push towards the electromagnetic near-field region such as those where the use of very large antenna arrays is envisioned. Motivated by this consideration, we show how physical principles can be used to derive a channel model that is also valid in the electromagnetic near-field. We show that wave propagation through a three-dimensional scattered medium can be generally modeled as a linear and space-variant system. We first review the physics principles that lead to a closed-form deterministic angular representation of the channel response. This serves as a basis for deriving a stochastic representation of the channel in terms of statistically independent Gaussian random coefficients for randomly spatially-stationary propagation environments. The very desirable property of spatial stationarity can always be retained by excluding reactive propagation mechanisms confined in the extreme near-field propagation region. Remarkably, the provided stochastic representation is directly connected to the Fourier spectral representation of a general spatially-stationary random field.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge