MRT-based Joint Unicast and Multigroup Multicast Transmission in Massive MIMO Systems
Paper and Code
Dec 31, 2021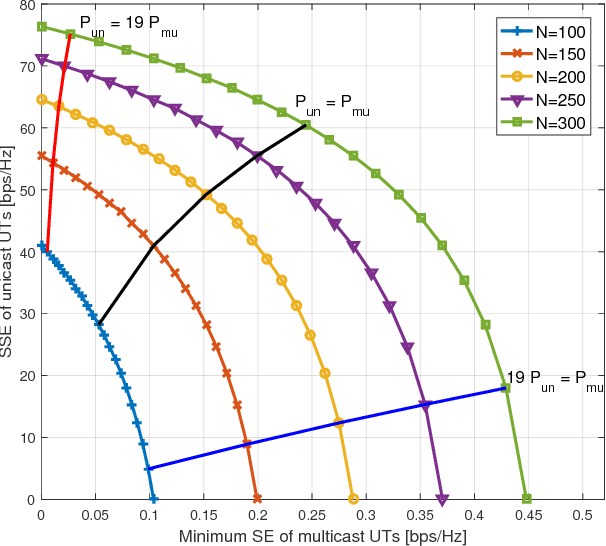
We study joint unicast and multigroup multicast transmission in single-cell massive multiple-input-multiple-output (MIMO) systems, under maximum ratio transmission. For the unicast transmission, the objective is to maximize the weighted sum spectral efficiency (SE) of the unicast user terminals (UTs) and for the multicast transmission the objective is to maximize the minimum SE of the multicast UTs. These two problems are coupled to each other in a conflicting manner, due to their shared power resource and interference. To address this, we formulate a multiobjective optimization problem (MOOP). We derive the Pareto boundary of the MOOP analytically and determine the values of the system parameters to achieve any desired Pareto optimal point. Moreover, we prove that the Pareto region is convex, hence the system should serve the unicast and multicast UTs at the same time-frequency resource.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge