Thomas Christie
Misconception Diagnosis From Student-Tutor Dialogue: Generate, Retrieve, Rerank
Feb 02, 2026Abstract:Timely and accurate identification of student misconceptions is key to improving learning outcomes and pre-empting the compounding of student errors. However, this task is highly dependent on the effort and intuition of the teacher. In this work, we present a novel approach for detecting misconceptions from student-tutor dialogues using large language models (LLMs). First, we use a fine-tuned LLM to generate plausible misconceptions, and then retrieve the most promising candidates among these using embedding similarity with the input dialogue. These candidates are then assessed and re-ranked by another fine-tuned LLM to improve misconception relevance. Empirically, we evaluate our system on real dialogues from an educational tutoring platform. We consider multiple base LLM models including LLaMA, Qwen and Claude on zero-shot and fine-tuned settings. We find that our approach improves predictive performance over baseline models and that fine-tuning improves both generated misconception quality and can outperform larger closed-source models. Finally, we conduct ablation studies to both validate the importance of our generation and reranking steps on misconception generation quality.
laplax -- Laplace Approximations with JAX
Jul 22, 2025

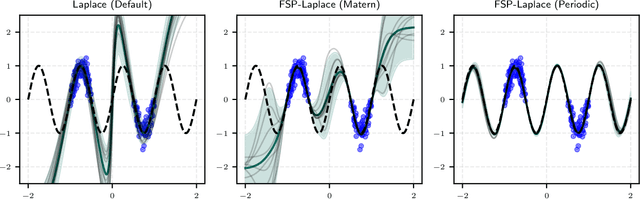

Abstract:The Laplace approximation provides a scalable and efficient means of quantifying weight-space uncertainty in deep neural networks, enabling the application of Bayesian tools such as predictive uncertainty and model selection via Occam's razor. In this work, we introduce laplax, a new open-source Python package for performing Laplace approximations with jax. Designed with a modular and purely functional architecture and minimal external dependencies, laplax offers a flexible and researcher-friendly framework for rapid prototyping and experimentation. Its goal is to facilitate research on Bayesian neural networks, uncertainty quantification for deep learning, and the development of improved Laplace approximation techniques.
Higher-Order Expander Graph Propagation
Nov 14, 2023Abstract:Graph neural networks operate on graph-structured data via exchanging messages along edges. One limitation of this message passing paradigm is the over-squashing problem. Over-squashing occurs when messages from a node's expanded receptive field are compressed into fixed-size vectors, potentially causing information loss. To address this issue, recent works have explored using expander graphs, which are highly-connected sparse graphs with low diameters, to perform message passing. However, current methods on expander graph propagation only consider pair-wise interactions, ignoring higher-order structures in complex data. To explore the benefits of capturing these higher-order correlations while still leveraging expander graphs, we introduce higher-order expander graph propagation. We propose two methods for constructing bipartite expanders and evaluate their performance on both synthetic and real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge