Variational Inference of overparameterized Bayesian Neural Networks: a theoretical and empirical study

This paper studies the Variational Inference (VI) used for training Bayesian Neural Networks (BNN) in the overparameterized regime, i.e., when the number of neurons tends to infinity. More specifically, we consider overparameterized two-layer BNN and point out a critical issue in the mean-field VI training. This problem arises from the decomposition of the lower bound on the evidence (ELBO) into two terms: one corresponding to the likelihood function of the model and the second to the Kullback-Leibler (KL) divergence between the prior distribution and the variational posterior. In particular, we show both theoretically and empirically that there is a trade-off between these two terms in the overparameterized regime only when the KL is appropriately re-scaled with respect to the ratio between the the number of observations and neurons. We also illustrate our theoretical results with numerical experiments that highlight the critical choice of this ratio.

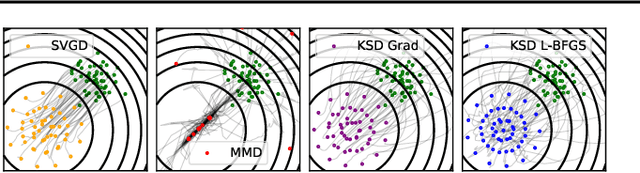
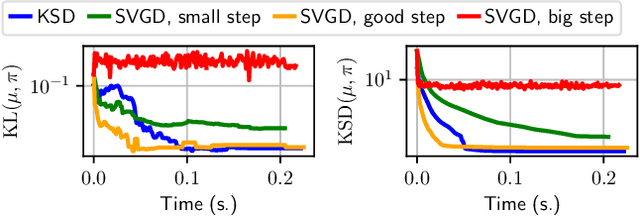
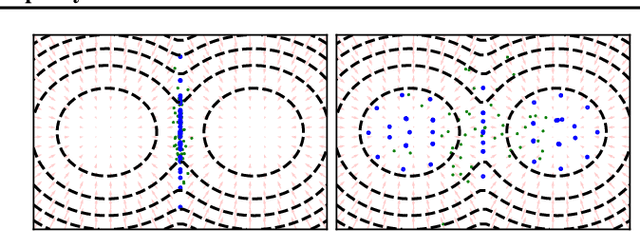
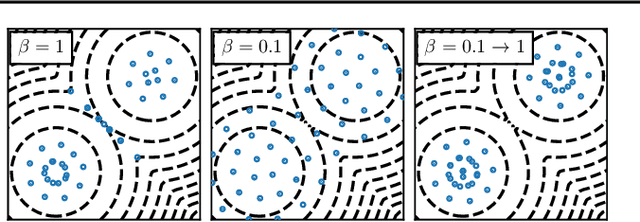
Kernel Stein Discrepancy Descent

Among dissimilarities between probability distributions, the Kernel Stein Discrepancy (KSD) has received much interest recently. We investigate the properties of its Wasserstein gradient flow to approximate a target probability distribution $\pi$ on $\mathbb{R}^d$, known up to a normalization constant. This leads to a straightforwardly implementable, deterministic score-based method to sample from $\pi$, named KSD Descent, which uses a set of particles to approximate $\pi$. Remarkably, owing to a tractable loss function, KSD Descent can leverage robust parameter-free optimization schemes such as L-BFGS; this contrasts with other popular particle-based schemes such as the Stein Variational Gradient Descent algorithm. We study the convergence properties of KSD Descent and demonstrate its practical relevance. However, we also highlight failure cases by showing that the algorithm can get stuck in spurious local minima.

Minibatch optimal transport distances; analysis and applications

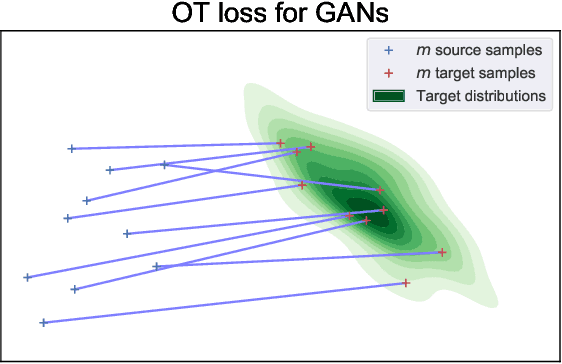
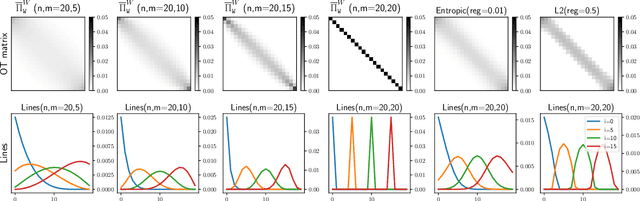
Optimal transport distances have become a classic tool to compare probability distributions and have found many applications in machine learning. Yet, despite recent algorithmic developments, their complexity prevents their direct use on large scale datasets. To overcome this challenge, a common workaround is to compute these distances on minibatches i.e. to average the outcome of several smaller optimal transport problems. We propose in this paper an extended analysis of this practice, which effects were previously studied in restricted cases. We first consider a large variety of Optimal Transport kernels. We notably argue that the minibatch strategy comes with appealing properties such as unbiased estimators, gradients and a concentration bound around the expectation, but also with limits: the minibatch OT is not a distance. To recover some of the lost distance axioms, we introduce a debiased minibatch OT function and study its statistical and optimisation properties. Along with this theoretical analysis, we also conduct empirical experiments on gradient flows, generative adversarial networks (GANs) or color transfer that highlight the practical interest of this strategy.

Sliced-Wasserstein Flows: Nonparametric Generative Modeling via Optimal Transport and Diffusions

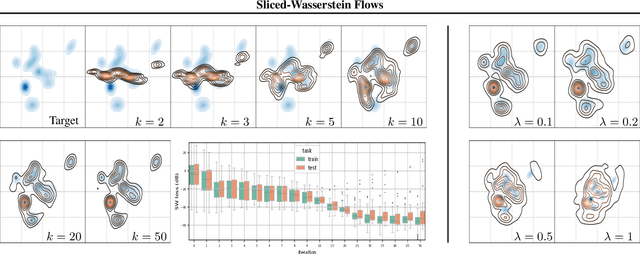
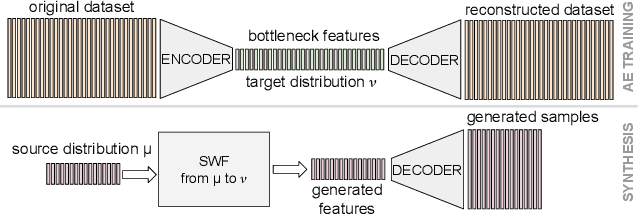
By building up on the recent theory that established the connection between implicit generative modeling and optimal transport, in this study, we propose a novel parameter-free algorithm for learning the underlying distributions of complicated datasets and sampling from them. The proposed algorithm is based on a functional optimization problem, which aims at finding a measure that is close to the data distribution as much as possible and also expressive enough for generative modeling purposes. We formulate the problem as a gradient flow in the space of probability measures. The connections between gradient flows and stochastic differential equations let us develop a computationally efficient algorithm for solving the optimization problem, where the resulting algorithm resembles the recent dynamics-based Markov Chain Monte Carlo algorithms. We provide formal theoretical analysis where we prove finite-time error guarantees for the proposed algorithm. Our experimental results support our theory and shows that our algorithm is able to capture the structure of challenging distributions.

Analysis of Langevin Monte Carlo via convex optimization

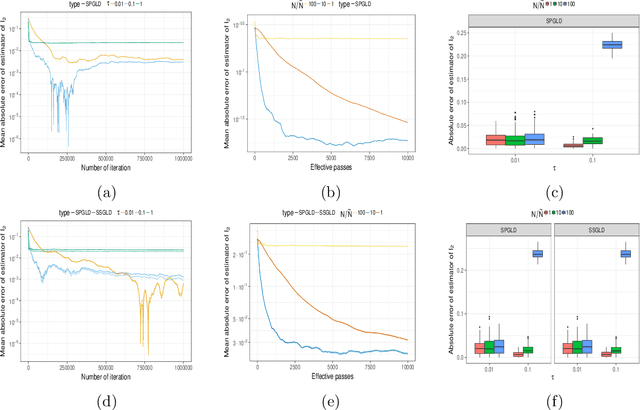
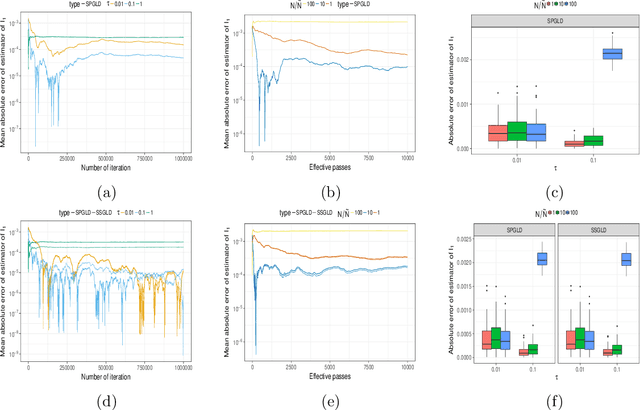
In this paper, we provide new insights on the Unadjusted Langevin Algorithm. We show that this method can be formulated as a first order optimization algorithm of an objective functional defined on the Wasserstein space of order $2$. Using this interpretation and techniques borrowed from convex optimization, we give a non-asymptotic analysis of this method to sample from logconcave smooth target distribution on $\mathbb{R}^d$. Based on this interpretation, we propose two new methods for sampling from a non-smooth target distribution, which we analyze as well. Besides, these new algorithms are natural extensions of the Stochastic Gradient Langevin Dynamics (SGLD) algorithm, which is a popular extension of the Unadjusted Langevin Algorithm. Similar to SGLD, they only rely on approximations of the gradient of the target log density and can be used for large-scale Bayesian inference.